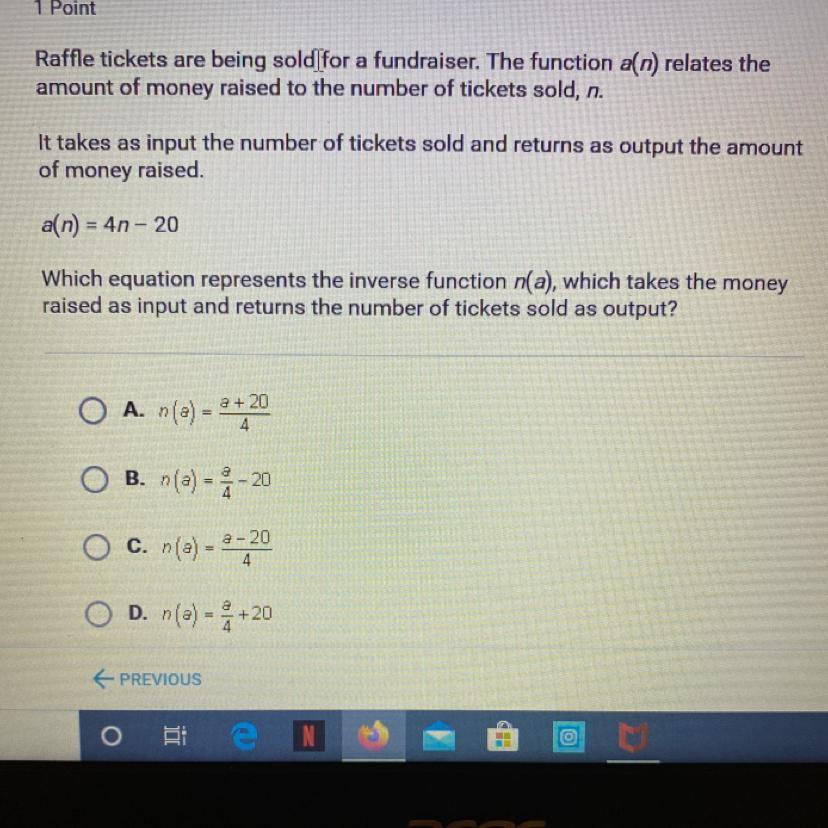
a(n) = 4n - 20
Which equation represents the inverse function n(a), which takes the money
raised as input and returns the number of tickets sold as output?

Correct question:

The vector matrix [ [tex] \left[\begin{array}{ccc}2\\7\end{array}\right] [/tex] is dilated by a factor of 1.5 and then reflected across the x axis. If the resulting matrix is [a/b] then a=??? and b=???

Answer:

a = 3

b = 10.5

Step-by-step explanation:

Given:

Vector matrix = [tex] \left[\begin{array}{ccc}2\\7\end{array}\right] [/tex]

Dilation factor = 1.5

Since the vector matrix is dilated by 1.5, we have:

[tex] \left[\begin{array}{ccc}1.5 * 2\\1.5 * 7\end{array}\right] [/tex]

= [tex] \left[\begin{array}{ccc}3\\10.5\end{array}\right] [/tex]

Here, we are told the vector is reflected on the x axis.

Therefore,

a = 3

b = 10.5

Answer:

a = 3

b = -10.5

Step-by-step explanation:

got a 100% on PLATO

Answer: x = 15, y = 12.5

Step-by-step explanation:

The sum of the three angle measures of a triangle equals 180ᴼ

Since these triangles are vertical, the measures are congruent.

45 + 60 = 105

180 - 105 = 75

So now we know that 5x = 75ᴼ and 6y = 75ᴼ.

To find x, divide 75 by 5

75 / 5 = 15

x = 15

To find y, divide 75 by 6

75 / 6 = 12.5

y = 12.5

Answer:  B) 110

Step-by-step explanation:

It is stated that DE and XY are parallel.

Therefore, 110° and x° are Corresponding Angles, which means they are congruent (equal).

110° = x°

110 = x

Answer:

The phrase "95% confident" means that there is a 95% confidence that the true mean parking time of students from within the various college on campus is included in the interval (9.1944, 11.738).

Step-by-step explanation:

The (1 - α)% confidence interval for population parameter implies that there is a (1 - α) probability that the true value of the parameter is included in the interval.

Or, the (1 - α)% confidence interval for the parameter implies that there is (1 - α)% confidence or certainty that the true parameter value is contained in the interval.

From the provided data the 95% confidence interval for the population mean parking time of students from within the various college on campus is:

CI = (9.1944, 11.738)

This 95% confidence interval implies that the true mean parking time of students from within the various college on campus is included in the interval (9.1944, 11.738) with a specific probability or confidence of 95%.

Thus, the phrase "95% confident" means that there is a 95% confidence that the true mean parking time of students from within the various college on campus is included in the interval (9.1944, 11.738).

Answer:

inside, 120

Step-by-step explanation:

Answer:

1. Inside

2. 120

did on edge

Answer:

47.5%.

Step-by-step explanation:

60 is 2 standard deviations below the mean.

According to the emperical rule, there is approximately 90% of normally distributed  data within 2 standard deviations of the mean. Your interval is half of  that because it is the data between the mean and two standard deviations

below the mean. therefore, the answer is 47.5%.

The percentage of scores that lie between 60 and 80 is 47.75%

Z score is used to determine by how many standard deviations the raw score is above or below the mean. The z score is given by:

[tex]z=\frac{x-\mu}{\sigma} \\\\where\ x=raw\ score,\mu=mean, \sigma=standard\ deviation[/tex]

Given that:

μ = 80, σ = 10

[tex]For\ x=60:\\\\z=\frac{60-80}{10} =-2\\\\For\ x=80:\\\\z=\frac{80-80}{10} =0[/tex]

P(60 < x < 80) = P(-2 < z < 0) = P(z < 0) - P(z < -2) = 0.5 - 0.0228 = 47.75%

Find out more at: https://brainly.com/question/15016913

Answer:

  x² = 32² +35² -2·32·35·cos(120°)

Step-by-step explanation:

The equation of choice is the one that makes use of the law of cosines. If x represents the unknown side, then you would want to solve ...

  x² = 32² +35² -2·32·35·cos(120°)

_____

The solution is ...

  x² = 3369

  x = √3369 ≈ 58.043

_____

Comment on the question

Usually, when the question asks, "Which ...", there will be a selection of answer choices. Those will give a clue as to what variables are used, how far the equation is simplified, and whether the equation is for x² or for x. That information is not provided here, so we have shown the equation we would use to solve the problem.

Answer:

The guy above me is right.

Step-by-step explanation:

I took the test.

Answer:

A) Brown-Brown ,Brown-Blue, Blue-Brown, Blue-Blue  B) 1/4 =0,25   C)3/4=0,75

Step-by-step explanation:

Lets mother's  "BROWN" is  "BROWN-M",  

mother's "BLUE"  is  " BLUE-M"

Lets  father's  "BROWN" is "BROWN-F" and

father's  "BLUE " is  "BLUE-F"

The kid can have the genotype as follows (list of possible outcomes) :

1. BROWN-M>BROWN-F   ( received BROWN as from mother as from father)

2. BROWN-M>BLUE-F  ( Received BROWN from mother and BLUE from father)

3. BLUE-M>BROWN-F ( Received BLUE from mother and Brown from father)

4.  BLUE-M>BLUE-F ( Received BLUE as from mother as from father)

b) As we can see in a) only 1 outcome from 4 is BLUE-BLUE.  So the probability of BLUE-BLUE genotype is

P(BLUE>BLUE)=1/4=0.25  

c) As we know that if the child has at least one brown allele, that color will dominate and the eyes will be brown.

It means that outcomes BROWN-BROWN, BROWN-BLUE and BLUE-BROWN determine brown color of eye. So the number of these outcomes is 3. Total amount of outcomes is 4.

So probability that eyes are brown is P(Brown eyes)=3/4 =0.75

Answer:

10 rows with 6 passengers per row

Step-by-step explanation:

Let x be the number of rows and y the number of passengers per row.

Then we can interpret the story as the following two equations:

xy=60

(x+2)(y-1)=60

Solving these two equations:

y=60/x

(x+2)(60/x-1)=60     (substitute y)

60 - x + 120/x - 2 = 60 (multiply by -x)

x² + 2x - 120 = 0     (factor)

(x-10)(x+12) = 0

x = 10

y = 60/10 = 6

and indeed 10 * 6 = 60 and also 12 * 5 = 60

Answer:

A(s) = 255.8857

Step-by-step explanation:

Find the area of the surface correct to four decimal places by expressing the area in terms of a single integral and using your calculator to estimate the integral. The part of the surface z = e^-x^2-y^2 that lies above the disk x2 + y2 ≤ 81.

Given that:

[tex]Z = e^{-x^2-y^2}[/tex]

By applying rule; the partial derivatives with respect to x and y

[tex]\dfrac{\partial z }{\partial x}= -2xe^{-x^2-y^2}[/tex]

[tex]\dfrac{\partial z }{\partial y}= -2ye^{-x^2-y^2}[/tex]

The integral over the general region D with respect to x and y is :

[tex]A(s) = \int \int _D \sqrt{1+(\dfrac{\partial z}{\partial x} )^2 +(\dfrac{\partial z}{\partial y} )^2 }\ dA[/tex]

[tex]A(s) = \int \int _D \sqrt{1+(-2xe^{-x^2-y^2})^2 +(-2ye^{-x^2-y^2})^2 } \ dA[/tex]

[tex]A(s) = \int \int _D \sqrt{1+4x^2({e^{-x^2-y^2})^2 +4y^2({e^{-x^2-y^2}})^2 }} \ dA[/tex]

[tex]A(s) = \int \int _D \sqrt{1+(4x^2+4y^2)({e^{-x^2-y^2})^2 }} \ dA[/tex]

[tex]A(s) = \int \int _D \sqrt{1+(4x^2+4y^2)e^{-2}({{x^2+y^2}) }} \ dA[/tex]

By relating the equation to cylindrical coordinates

[tex]A(s) = \int \int_D \sqrt{1+4r^2 e^{-2r^2} }. rdA[/tex]

The bounds for integration for the circle within the cylinder [tex]x^2+y^2 =81[/tex] is r =9

[tex]A(s) = \int \limits ^{2 \pi}_{0} \int \limits^9_0 r \sqrt{1+4r^2 e^{-2r^2} }. dr d\theta[/tex]

[tex]A(s) = {2 \pi} \int \limits^9_0 r \sqrt{1+4r^2 e^{-2r^2} }\ dr[/tex]

Using integral calculator to estimate the  integral,we have:

A(s) = 255.8857

Answer:

21.7 metres (assuming the triangle is a right triangle)

Step-by-step explanation:

Assuming this is a right triangle, we can simply use the Pythagorean Theorem, which states that in a right triangle with legs a and b and hypotenuse c:

a² + b² = c²

Here, a = 20, b = 8.5, and R = c. Plug these in:

a² + b² = c²

20² + 8.5² = R²

400 + 72.25 = R²

472.25 = R²

R = √472.25 ≈ 21.7 m

Thus, R is about 21.7 metres.

~ an aesthetics lover

Answer:

The curvature is modelled by [tex]\kappa = \frac{e^{-t}}{6\sqrt{2}}[/tex].

Step-by-step explanation:

The equation of the curvature is:

[tex]\kappa = \frac{|\dot {x}\cdot \ddot {y}-\dot{y}\cdot \ddot{x}|}{[\dot{x}^{2}+\dot{y}^{2}]^{\frac{3}{2} }}[/tex]

The parametric componentes of the curve are:

[tex]x = 6\cdot e^{t} \cdot \cos t[/tex] and [tex]y = 6\cdot e^{t}\cdot \sin t[/tex]

The first and second derivative associated to each component are determined by differentiation rules:

First derivative

[tex]\dot{x} = 6\cdot e^{t}\cdot \cos t - 6\cdot e^{t}\cdot \sin t[/tex] and [tex]\dot {y} = 6\cdot e^{t}\cdot \sin t + 6\cdot e^{t} \cdot \cos t[/tex]

[tex]\dot x = 6\cdot e^{t} \cdot (\cos t - \sin t)[/tex] and [tex]\dot {y} = 6\cdot e^{t}\cdot (\sin t + \cos t)[/tex]

Second derivative

[tex]\ddot{x} = 6\cdot e^{t}\cdot (\cos t-\sin t)+6\cdot e^{t} \cdot (-\sin t -\cos t)[/tex]

[tex]\ddot x = -12\cdot e^{t}\cdot \sin t[/tex]

[tex]\ddot {y} = 6\cdot e^{t}\cdot (\sin t + \cos t) + 6\cdot e^{t}\cdot (\cos t - \sin t)[/tex]

[tex]\ddot{y} = 12\cdot e^{t}\cdot \cos t[/tex]

Now, each term is replaced in the the curvature equation:

[tex]\kappa = \frac{|6\cdot e^{t}\cdot (\cos t - \sin t)\cdot 12\cdot e^{t}\cdot \cos t-6\cdot e^{t}\cdot (\sin t + \cos t)\cdot (-12\cdot e^{t}\cdot \sin t)|}{\left\{\left[6\cdot e^{t}\cdot (\cos t - \sin t)\right]^{2}+\right[6\cdot e^{t}\cdot (\sin t + \cos t)\left]^{2}\right\}^{\frac{3}{2}}} }[/tex]

And the resulting expression is simplified by algebraic and trigonometric means:

[tex]\kappa = \frac{72\cdot e^{2\cdot t}\cdot \cos^{2}t-72\cdot e^{2\cdot t}\cdot \sin t\cdot \cos t + 72\cdot e^{2\cdot t}\cdot \sin^{2}t+72\cdot e^{2\cdot t}\cdot \sin t \cdot \cos t}{[36\cdot e^{2\cdot t}\cdot (\cos^{2}t -2\cdot \cos t \cdot \sin t +\sin^{2}t)+36\cdot e^{2\cdot t}\cdot (\sin^{2}t+2\cdot \cos t \cdot \sin t +\cos^{2} t)]^{\frac{3}{2} }}[/tex]

[tex]\kappa = \frac{72\cdot e^{2\cdot t}}{[72\cdot e^{2\cdot t}]^{\frac{3}{2} } }[/tex]

[tex]\kappa = [72\cdot e^{2\cdot t}]^{-\frac{1}{2} }[/tex]

[tex]\kappa = 72^{-\frac{1}{2} }\cdot e^{-t}[/tex]

[tex]\kappa = \frac{e^{-t}}{6\sqrt{2}}[/tex]

The curvature is modelled by [tex]\kappa = \frac{e^{-t}}{6\sqrt{2}}[/tex].

Answer:

0.15%

Step-by-step explanation:

3 standard deviations encompasses 99.7% of the data symmetrically around the mean with 0.15% on each side that is above and below. so above would be 0.15%

The percentage of the adult male population s taller than the average basketball player is 0.15%. This option A is correct.

If their heights are distributed with a mean of 70 inches the SD of 3 inches and the average play is 79 inches stated by the empirical rule. The average population should be 0.15% by the rule.

Based on the standard deviation that shows the three deviations that includes 99.7% of the data symmetrically with the mean of 0.15% on each side hence i.e above and below.

Usin the standardize x to z = (x - μ) / σ, we get 79-70 / 3  as 0.15

Find out more information about the heights.

brainly.com/question/1674508.

Answer:

The probability of the combination {H, T and H} is 0.125.

Step-by-step explanation:

The sample space of flipping a quarter is:

S = {H and T}

The probability of both outcomes is same, i.e. P (H) = P (T) = 0.50.

It is provided that three quarters are flipped one at a time.

The outcomes of all the three quarters are independent of each other.

Compute the probability of the combination {H, T and H} as follows:

[tex]P(\text{H},\text{T and H}) = P(\text{H})\times P(\text{T})\times P(\text{H})[/tex]

                        [tex]=0.50\times 0.50\times 0.50\\=0.125[/tex]

Thus, the probability of the combination {H, T and H} is 0.125.

Answer:

1320 ways

Step-by-step explanation:

To solve we need to use permutations and factorials. If we wanted to find where they would all place 1-12, we would do 12!

12! is the same as 12x11x10x9x8... etc

But in this problem, we are only looking for the top 3.

We can set up a formula

[tex]\frac{n!}{(n-r)!}[/tex]

N is the number of options that are available and r represents the amount we are choosing

In this case, we have 12 teams so n=12

We are looking for the top 3 so r=3

[tex]\frac{12!}{(12-3)!}[/tex]

[tex]\frac{12!}{9!}[/tex]

We expand the equation and cancel out

[tex]\frac{12x11x10x9x8x7x6x5x4x3x2}{9x8x7x6x5x4x3x2}[/tex]

Notice how both sides can cancel out every number 9 and below

That leaves us with 12x11x10

1320 ways

The possible ways for the gold, silver, and bronze medals to be awarded is 1320

A permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements.

The word "permutation" also refers to the act or process of changing the linear order of an ordered set.

Given that, there are 12 teams, each representing a different country, in a women’s Olympic basketball tournament.

We need to find that, in how many ways is it possible for the gold, silver, and bronze medals to be awarded,

Using the concept of permutation, to find the number of ways

ⁿPₓ = n!/(n-x)!

= 12! / (12-3)!

= 12! / 9!

= 1320

Hence, the possible ways for the gold, silver, and bronze medals to be awarded is 1320

Learn more about permutation click;

https://brainly.com/question/30649574

#SPJ7

Group of answer choices:

A) 0.56 to 0.68

B) 0.52 to 0.72

C) 0.53 to 0.71

D) 0.55 to 0.69

Answer:

Option  B) 0.52 to 0.72

Step-by-step explanation:

This is a very trivial exercise. A very good point that is required to solve this question is that the wider the Confidence level, the wider the Confidence Interval.

Let us consider the options one after the other for the width of interval:

Option A) 0.56 to 0.68

Width of Interval = 0.68 - 0.56 = 0.12

Option  B) 0.52 to 0.72

Width of Interval = 0.72 - 0.52 = 0.20

Option  C) 0.53 to 0.71

Width of Interval = 0.71 - 0.53 = 0.18

Option D) 0.55 to 0.69

Width of Interval = 0.69 - 0.55 = 0.14

Assigning the confidence level based on the width of the confidence intervals:

Option A) 0.56 to 0.68 = 90%

Option D) 0.55 to 0.69 = 95%

Option  C) 0.53 to 0.71  = 98%

Option  B) 0.52 to 0.72  = 99%

Answer:

Solution,

Complement of 70°

=90°-70°

=20°

hope this helps...

Good luck on your assignment..

Answer:

20°

Step-by-step explanation:

Complement of 70° is 90°-70°= 20°  

To determine the complement, subtract the given angle from 90.

Answer:

4

Step-by-step explanation:

C1= 2π*8= 16π

C2= 2π*2= 4π

C1/C2= 16π/4π= 4

Answer:

4

Step-by-step explanation:

The circumference is pi*d.

pi*16/pi*4

Cancel pi.

16/4

= 4

Answer:

(B) 25%

Step-by-step explanation:

Answer:

3780 different words

Step-by-step explanation:

The number of possible words that can be formed by a word with n letters is given by n! (factorial of n), but when we have repeated letters, we need to divide the result by the factorial of each number of repeated letters.

In this case, we have 9 letters, but we have 4 times A, 2 times B and 2 times C, so the formula to calculate the number of different words is:

[tex]number = {9!}/(4!2!2!)[/tex]

[tex]number = (9*8*7*6*5*4*3*2)/(4*3*2*2*2)[/tex]

[tex]number = 3780\ words[/tex]

So we can form 3780 different words.

The value of root 10 is between 3 and 3.5

Answer:

The answer is below

Step-by-step explanation:

What we should do is the following:

First, from the random sample of 852 researchers, it is necessary to obtain the number of adult residents who consumed alcohol in the past year.

After the above, we must calculate the proportion of adult residents who consumed alcohol in the last year by dividing the number of adult residents who consumed alcohol in the last year by 852.

After this, we must compare if the proportion is exactly 70% or different from it.

We have the following hypotheses:

Null Hypothesis: The proportion of adult residents who consumed alcohol in the last year in the state of Wisconsin is exactly 70%

Alternative hypothesis: The proportion of adult residents who consumed alcohol in the last year in the state of Wisconsin is not equal to 70%

Answer:

5/7

Step-by-step explanation:

4/7 < x < 6/7

Let x be the middle value of 4/7 and 6/7.

(4/7 + 6/7)/2

(10/7)/2

10/14 = 5/7

4/7 < 5/7 < 6/7

Answer:

A = 201.0619298 cm^2

Step-by-step explanation:

The area of a circle is given by

A  = pi r^2

A = pi ( 8) ^2

A = 64 pi

Letting pi = pi button

A = 201.0619298 cm^2

Answer:

Step-by-step explanation:

Area of a circle is πr²

where r is the radius

From the question r = 8cm

So the area of the circle is

π(8)²

= 64π

= 201.061

Hope this helps you

Answer:

Step-by-step explanation:

Everything to know about a and b!

Graph the parabola using the direction, vertex, focus, and axis of symmetry.

Direction: Opens Up

Vertex: (0, −5)

Focus: (0, [tex]-\frac{19}{4\\}[/tex]−)

Axis of Symmetry: x = 0

Directrix: y = [tex]-\frac{21}{4}[/tex]

For Part b

Table:

x    |     y

______

−2      −1

−1      −4

0       −5

1        −4

2       −1

Answer:

  30 miles

Step-by-step explanation:

Jose's charges are ...

  j = 5 + 0.30m . . . . . for m miles

Kathy's charges are ...

  k = 8 +0.20m . . . . . for m miles

The charges are the same when ...

 j = k

  5 +0.30m = 8 + 0.20m

  0.30m = 3 + 0.20m . . . . subtract 5

  0.10m = 3 . . . . . . . . . . . . subtract 0.20m

  m = 30 . . . . . . . . . . . . . . . multiply by 10

The charges will be the same for a distance of 30 miles.

Answer:

[tex] y = -6x^2 -17 x -12[/tex]

And since the higher exponent for the x term is 2 we can classify the equation  as quadratic

Quadratic term: -6

Linear term: -17

Constant term: -12

Step-by-step explanation:

For this problem we have the following equation:

[tex] y = (3x+4)(-2x-3)[/tex]

And we can distribute the terms and we got:

[tex] y = -6x^2 -9x -8x -12[/tex]

And solving we got:

[tex] y = -6x^2 -17 x -12[/tex]

And since the higher exponent for the x term is 2 we can classify the equation  as quadratic

Quadratic term: -6

Linear term: -17

Constant term: -12

Answer:

Step-by-step explanation:

Given that:

[tex]E( \hat \theta _1) = \theta \ \ \ \ E( \hat \theta _2) = \theta \ \ \ \ V( \hat \theta _1) = \sigma_1^2 \ \ \ \ V(\hat \theta_2) = \sigma_2^2[/tex]

If we are to consider the estimator [tex]\hat \theta _3 = a \hat \theta_1 + (1-a) \hat \theta_2[/tex]

a. Then, for  [tex]\hat \theta_3[/tex] to be an unbiased estimator ; Then:

[tex]E ( \hat \theta_3) = E ( a \hat \theta_1+ (1-a) \hat \theta_2)[/tex]

[tex]E ( \hat \theta_3) = aE ( \theta_1) + (1-a) E ( \hat \theta_2)[/tex]

[tex]E ( \hat \theta_3) = a \theta + (1-a) \theta = \theta[/tex]

b) If [tex]\hat \theta _1 \ \ and \ \ \hat \theta_2[/tex] are independent

[tex]V(\hat \theta _3) = V (a \hat \theta_1+ (1-a) \hat \theta_2)[/tex]

[tex]V(\hat \theta _3) = a ^2 V ( \hat \theta_1) + (1-a)^2 V ( \hat \theta_2)[/tex]

Thus; in order to minimize the variance of [tex]\hat \theta_3[/tex] ; then constant a can be determined as :

[tex]V( \hat \theta_3) = a^2 \sigma_1^2 + (1-a)^2 \sigma^2_2[/tex]

Using differentiation:

[tex]\dfrac{d}{da}(V \ \hat \theta_3) = 0 \implies 2a \ \sigma_1^2 + 2(1-a)(-1) \sigma_2^2 = 0[/tex]

⇒

[tex]a (\sigma_1^2 + \sigma_2^2) = \sigma^2_2[/tex]

[tex]\hat a = \dfrac{\sigma^2_2}{\sigma^2_1+\sigma^2_2}[/tex]

This implies that

[tex]\dfrac{d}{da}(V \ \hat \theta_3)|_{a = \hat a} = 2 \ \sigma_1^2 + 2 \ \sigma_2^2 > 0[/tex]

So, [tex]V( \hat \theta_3)[/tex] is minimum when [tex]\hat a = \dfrac{\sigma_2^2}{\sigma_1^2+\sigma_2^2}[/tex]

As such; [tex]a = \dfrac{1}{2}[/tex]       if   [tex]\sigma_1^2 \ \ = \ \ \sigma_2^2[/tex]

Answer:

Step-by-step explanation:

Step1 : Verify Sn is valid for n = 1

Step-by-step explanation:

6

[tex]6 \sqrt{6} [/tex]

Answer:

6√6is the exact answer