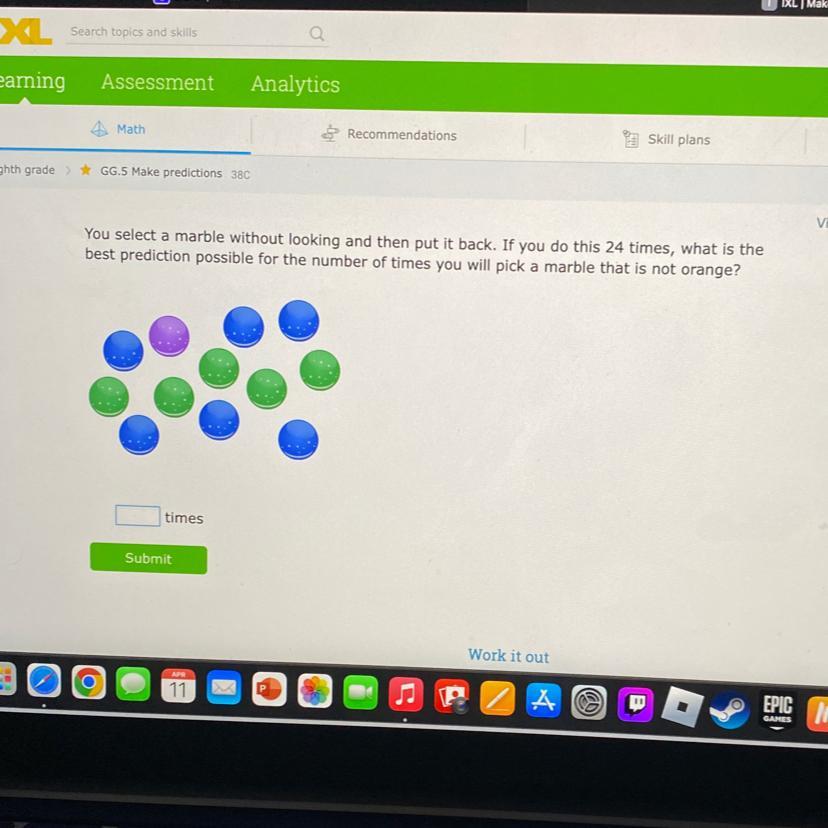
You select a marble without looking and then put it back. If you do this 24 times, what is the
best prediction possible for the number of times you will pick a marble that is not orange?
times

The range of f include the following: D. -5 ≤ f(x) ≤ 5.

In Mathematics and Geometry, a domain is the set of all real numbers for which a particular function is defined.

Additionally, the vertical extent of any graph of a function represents all range values and they are always read and written from smaller to larger numerical values, and from the bottom of the graph to the top.

By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:

Domain = {-6, 5} or -6 ≤ x ≤ 5.

Range = {-5, 5} or -5 ≤ f(x) ≤ 5.

Read more on domain here: brainly.com/question/17440903

#SPJ1

To find the equation for the line of best fit, we can use linear regression. Based on the given data:

x: 2, 5, 7, 12, 16

y: 9, 10, 5, 3, 2

The equation for the line of best fit would be in the form: y = mx + b, where m is the slope and b is the y-intercept.

Using a calculator or statistical software, we can calculate the slope and y-intercept for the line of best fit.

The result is:

Slope (m): -0.580 (rounded to three decimal places) Y-intercept (b): 10.671 (rounded to three decimal places)

So, the correct answer is:

A. y = -0.580x + 10.671

The total surface area of the given figure is 619.2 in², which is not listed in the provided options.

The surface area is known to be measure of the total area occupied by the surface of the object. Defining the surface area mathematically in the presence of a curved surface is better than defining the arc length of a one-dimensional curve, or the surface area of ​​a polyhedron (i.e. an object with flat polygonal faces). Much more complicated. For a smooth surface sphere such as the following, surface area is assigned using representation as a parametric surface. This surface definition is based on calculus and includes partial derivatives and double integrals.

The triangular face of the given figure represent an equilateral triangle of sides 12 in.

Area of the triangle = (√3/4) × a²

Area of the triangular face:

= (√3/4) × 12²

= (√3/4) × 144

= 57.6 in²

Area of the rectangle = Length × width

Area of the rectangular face:

= 12 × 14

= 168 in²

Area of the given figure:

= (2 × 57.6) + (3 × 168)

= 115.2 + 504

= 619.2 in²

To know more about polygonal faces, visit:

https://brainly.com/question/16550007

#SPJ1

To determine the percent success, divide the actual score by the theoretical score, and then multiply the result by 100 to convert the value to a percentage.

We define the actual score, theoretical score, and explain how to calculate the percent success on an exam.
Actual score:

The actual score refers to the number of points a student has earned on an exam.

It represents the student's performance on the test, taking into account the correct and incorrect answers.
Theoretical score:

The theoretical score is the maximum number of points a student can earn on an exam.

This represents a perfect performance, where the student answers all questions correctly.
Calculating percent success:

To determine the percent success, divide the actual score by the theoretical score, and then multiply the result by 100 to convert the value to a percentage.
a. Divide the actual score by the theoretical score: (actual score) / (theoretical score)
b. Multiply the result by 100: (result from step a) * 100
c. The final value is the percent success.

For example, if a student has an actual score of 80 and the theoretical score is 100, the percent success would be calculated as follows:
a. 80 / 100 = 0.8
b. 0.8 * 100 = 80
c. The percent success is 80%.

For similar question on score.

https://brainly.com/question/29969863

#SPJ11

The power series method can be used to solve a nonhomogeneous differential equation about an ordinary point by finding both a homogeneous and particular solution using a series expansion and the method of undetermined coefficients.

The power series method is a technique used to find a series solution of a differential equation. When applied to a nonhomogeneous differential equation, the method involves finding both a homogeneous solution and a particular solution.

Assuming that the nonhomogeneous differential equation has the form

y''(x) + p(x)y'(x) + q(x)y(x) = f(x)

where p(x), q(x), and f(x) are functions of x, we can begin by finding the solution to the associated homogeneous equation

y''(x) + p(x)y'(x) + q(x)y(x) = 0

Using the power series method, we can assume a solution of the form:

y(x) = a0 + a1(x - x0) + a2(x - x0)^2 + ...

where a0, a1, a2, ... are constants to be determined, and x0 is the ordinary point of the differential equation.

Next, we can find the coefficients of the power series by substituting the series solution into the differential equation and equating coefficients of like powers of (x-x0). This leads to a system of equations for the coefficients, which can be solved iteratively.

After finding the homogeneous solution, we can find a particular solution using a similar method. Assuming a particular solution of the form:

y(x) = u(x) + v(x)

where u(x) is a solution to the associated homogeneous equation, and v(x) is a particular solution to the nonhomogeneous equation, we can use the method of undetermined coefficients to find v(x). This involves assuming a form for v(x) based on the form of f(x), and then solving for its coefficients using the same technique as before.

Once we have found both the homogeneous and particular solutions, we can combine them to obtain the general solution to the nonhomogeneous differential equation.

Learn more about nonhomogeneous differential equation here

brainly.com/question/30876746

#SPJ4

Answer:

26) 1.32

27) 90

28) 0.00845

29) 2.56x10^-1

30) 9.5x10^-3

31) 7.8x10

The actual height of the statue is option C 231.2 feet.

A scale factor is a number used in mathematics to scale or multiply a quantity or measurement by another factor in order to establish a proportional relationship between two identical figures or objects.

In other terms, the scale factor is the ratio of the corresponding lengths, widths, or heights of the two figures or objects if they are similar, that is, they have the same shape but may range in size. This implies that you may determine the dimension of the second object by multiplying one dimension of one object by the scale factor.

Given that the scale factor is 230:1.

Thus,

actual height of statue / 230 = height of drawing / 1.2 feet

Now,

actual height of statue = (1.2 feet / 1.2 feet) * 230

actual height of statue = 230 feet

Hence, the actual height of the statue is option C 231.2 feet.

Learn more about scale factor here:

https://brainly.com/question/29464385

#SPJ1

Answer:

Step-by-step explanation:

it is -2

Answer: -2

Step-by-step explanation:

So this is asking for the cube root of -8.

This is the same as asking what is multiplied by itself 3 times to get -8.

-2 * -2 *-2 = -8

You can also use a calculator.

Another way to solve it is to write -8^(1/3).

Hope this helps!!!

Answer: 102 miles.

Step-by-step explanation:

You divide 17 by 5 and then multiply by 30.

The minimum possible diameter of a soccer ball is 8.60 inches, and the maximum possible diameter is 8.70 inches.

What is equations?

Equivalent equations are algebraic equations that are having identical roots or solutions.

The soccer ball specifications require a diameter of 8.65 inches, with an allowable margin of error of 0.05 inch.

This means that the actual diameter of any new soccer ball should be within the range of 8.60 inches to 8.70 inches. The equation that can be used to find the diameter of a new soccer ball is d = 8.65 ± 0.05, where d represents the diameter. The symbol "±" indicates that the diameter can be either 0.05 inches larger or smaller than the specified diameter of 8.65 inches.

It is important to ensure that the diameter of a soccer ball falls within this allowable range to comply with the specifications and ensure fair play.

Therefore, The minimum possible diameter of a soccer ball is 8.60 inches, and the maximum possible diameter is 8.70 inches.

To know more about equations visit,

brainly.com/question/2972832

#SPJ1

In the given triangle, α is equal to 67.36°.

What is a triangle's definition?

A triangle is a two-dimensional closed geometric form that has three sides, three angles, and three vertices (corners). It is the most basic polygon, produced by joining any three non-collinear points in a plane. The sum all angles of a triangle is always 180°. Triangles are classed according to their side length (equilateral, isosceles, or scalene) and angle measurement (acute, right, or obtuse).

Now,

Using Trigonometric functions

We can use the sine function

So,

Sin α=Perpendicular/Hypotenuse

Sin α = 12/13

α=67.36°

Hence,

           The value of α will be 67.36°.

To know more about triangles visit the link

brainly.com/question/2773823

#SPJ1

16.) Mean average deviation= option C

17.) Range of a data set = option E.

18.) First quartile = opinion AB

19.) Second quartile = option B

20.) Third quartile = option A

21.) Interquartile range = option D

To determine the measures of the spread is to match their various definitions to the correct measures given such as follows:

16.) Mean average deviation: The average deviation of data from the mean.

17.) Range of a data set : The difference between the highest value and the lowest value in a numerical data set.

18.) First quartile: The median in the lower half.

19.) Second quartile: The median value in a data set.

20.) Third quartile: The median in the upper half.

21.) Interquartile range: The distance between the first and the third quartile.

Learn more about range here:

https://brainly.com/question/26098895

#SPJ1

Answer:  the solution for y in terms of x is y = (-1/4)x - 8.

Step-by-step explanation: In order to obtain a solution for y in the given equation of 4y = -x - 32, it is imperative to achieve the isolation of y on a singular side of the equation. To accomplish this task, it is possible to perform division on both sides of the equation by a factor of 4:

The given equation 4y/4 = (-x - 32)/4 can be expressed in an academic manner as follows: The given equation reveals that the quotient of 4y divided by 4 is equivalent to the quotient of the opposite of x added to negative 32, also divided by 4.

Upon performing simplification, the expression on the right-hand side yields:

The equation y = (-1/4)x - 8 can be expressed in an academic manner as follows: The dependent variable y is equivalent to the product of the constant (-1/4) and the independent variable x, with an additional decrement of eight.

The length of v, to the nearest 10th of a centimeter is 2.2.

To find the length of side v in triangle UVW, we can use the law of sines, which states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides and angles in the triangle.

Using this formula, we have,

v/sin(m∠V) = w/sin(m∠W)

We know that w = 1.4 cm and m∠W = 63°. To find sin(m∠W), we can use a calculator,

sin(63°) ≈ 0.89

Substituting the values we know into the formula, we get,

v/sin(m∠V) = 1.4/0.89

To solve for v, we need to find sin(m∠V). We know that the sum of the angles in a triangle is 180°, so we can find m∠V by subtracting the measures of the other two angles from 180°,

m∠V = 180° - m∠U - m∠W

m∠V = 180° - 29° - 63°

m∠V = 88°

Now, we can substitute the value of sin(m∠V) into the equation and solve for v,

v/ sin(88°) = 1.4/0.89

v ≈ 2.2 cm

Therefore, the length of side v in triangle UVW is approximately 2.2 cm to the nearest tenth of a centimeter.

To learn more about length here:

https://brainly.com/question/16537545

#SPJ4

Answer:

1.6

Step-by-step explanation: This is answer on DeltaMath

Answer:

Step-by-step explanation:

Medium is 28

Mean is 29

Range is 11

Midrange is 29.5

The statement "Poisson distributions are useful to model any variables positive or negative as long as they are integer values" is false because Poisson distributions are specifically used for modeling the number of events occurring in a fixed interval of time or space, given a fixed average rate of occurrence (λ).

The key characteristics of a Poisson distribution are:

1. The events are independent, meaning the occurrence of one event does not influence the occurrence of another event.
2. The average rate of occurrence (λ) is constant throughout the interval.
3. The probability of more than one event occurring in an infinitesimally small interval is negligible.

Given these characteristics, Poisson distributions are not suitable for modeling any variables, positive or negative, as long as they are integer values. Instead, they are applicable for modeling non-negative integer values (0, 1, 2, ...) representing the number of events occurring in a specific context. Negative integer values are not applicable in this distribution since it would be illogical to have negative events occurring in a fixed interval.

In summary, Poisson distributions are only useful for modeling non-negative integer values representing the number of events in a fixed interval of time or space, given a fixed average rate of occurrence.

You can learn more about Poisson distribution at: brainly.com/question/17280826

#SPJ11

Answer:

225 trains

Step-by-step explanation:

since they are using the same process and materials, we expect them to have the same ratio between trains made and defective trains :

600 / 30 = 20/1

one out of 20 is defect.

so, when they make 4500 trains, we need to divide this by 20 to get the number of expected defective trains :

4500 / 20 = 225

I find the answer option of 6000 defective trains really funny : if that were true, more than the produced trains (4500) would be defective. how ... ?

The solution to the equation 4,300e^(0.07x) - 123 = 5,000 for x is 2.5.

We can solve the equation 4,300e^(0.07x) - 123 = 5,000 for x by first adding 123 to both sides and then dividing both sides by 4,300 and taking the natural logarithm of both sides:

Using the above as a guide, we have the following:

4,300e^(0.07x) - 123 = 5,000

4,300e^(0.07x) = 5,123

e^(0.07x) = 5,123/4,300

e^(0.07x) = 1.1914

0.07x = ln(1.1914)

x = ln(1.1914)/0.07

Using a calculator, we get:

x ≈ 2.50

Rounding to the nearest tenth, the solution to the equation is approximately 2.5.

Read more about equation at

https://brainly.com/question/148035

#SPJ1

The inequality is simplified as 0 ≤ x ≤ 4

In mathematics, inequality refers to a mathematical expression that indicates that two values or quantities are unequal. An inequality is represented by the symbols "<" (less than), ">" (greater than), "≤" (less than or equal to), or "≥" (greater than or equal to).

For example, the inequality "x > 5" means that the value of x is greater than 5, and the inequality "y ≤ 10" means that the value of y is less than or equal to 10.

To graph the conjunction, we first need to solve for x:

-4 ≤ x - 4 ≤ 0

Add 4 to all parts of the inequality:

0 ≤ x ≤ 4

Image of graph is attached below.

To know more about conjunction, visit:

https://brainly.com/question/28839904

#SPJ1

The probability that a randomly selected carton has a puncture or a smashed corner is 0.076, or 7.6%.

What is probability?

Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.

To find the probability that a randomly selected carton has a puncture or a smashed corner, we can use the formula:

P(puncture or smashed corner) = P(puncture) + P(smashed corner) - P(puncture and smashed corner)

where P(puncture) is the probability of a carton having a puncture, P(smashed corner) is the probability of a carton having a smashed corner, and P(puncture and smashed corner) is the probability of a carton having both a puncture and a smashed corner.

Substituting the given probabilities into the formula, we get:

P(puncture or smashed corner) = 0.03 + 0.06 - 0.014

P(puncture or smashed corner) = 0.076

Therefore, the probability that a randomly selected carton has a puncture or a smashed corner is 0.076, or 7.6%.

To learn more about probability from the given link:

https://brainly.com/question/30034780

#SPJ1

Answer:

Step-by-step explanation:

The expected winning is $2.

To calculate the expected winning, we need to find the probability of each outcome and multiply it by the amount we will win in that outcome.

There are 2 possible outcomes for each coin flip: heads or tails. Therefore, there are 2x2x2=8 possible outcomes for flipping a coin three times.

Here are all the possible outcomes with the number of heads in each outcome:

The probability of each outcome can be calculated using the formula: probability = (number of favorable outcomes) / (total number of possible outcomes)

For example, the probability of getting 3 heads (HHH) is 1/8 because there is only one favorable outcome out of 8 possible outcomes.

Using this formula, we can calculate the probability and expected winning for each outcome:

To calculate the overall expected winning, we need to add up the expected winning for each outcome multiplied by its probability:

(1/8) x $6 + (1/4) x $4 + (1/4) x $4 + (1/4) x $4 + (3/8) x $2 + (3/8) x $2 + (3/8) x $2 + (1/8) x $0 = $2

Therefore, the expected winning is $2.

Learn more about probability

https://brainly.com/question/24756209

#SPJ4

Answer:

gcf is 'x'

Step-by-step explanation:

the common factor to the terms 'x²' and '3x' is 'x'

Answer: c=a2+b2

Step-by-step explanation:

The given triangles AOB and triangle OCB are proved congruent by using the property - angle side angle congruency.

Of three sides, three angles, plus three vertices, a triangle is a two-dimensional shape. If the matching sides or angles of two or more triangles match, the triangles are said to be congruent. Congruent triangles are identical in terms of their dimensions and shape.

Two triangles belong together if whose corresponding two angles but one included side are equivalent, according to the Angle- Side- Angle rule (ASA).

Given data:

As, AB || CD, ∠ABO ≅ ∠OCD (alternate interior angles)

∠AOB ≅ ∠COD (vertically opposite angles)

So,

∠AOB ≅ ∠COD

CO = OB

∠ABO ≅ ∠OCD

By using angle side angle congruence:

ΔAOB ≅ ΔCOD

Thus, the given triangles AOB and triangle OCB are proved congruent by using the property - angle side angle congruency.

know more about the triangle congruency:

https://brainly.com/question/3999145

#SPJ1

Answer:

x > 12

Step-by-step explanation:

3x + 18 > 54

Answer:

To find the density of the brick, we need to divide its mass by its volume:

density = mass / volume

Plugging in the values given in the problem, we get:

density = 2,022.75 g / 1,064.5 cm³

Simplifying the division, we get:

density = 1.8996 g/cm³

Rounding to the nearest tenth, we get:

density ≈ 1.9 g/cm³

Therefore, the density of the brick is approximately 1.9 grams per cubic centimeter (g/cm³).

Step-by-step explanation:

yes,because of SAS side angle side are equal.