WILL GIVE BRAINLIEST Which pairs of rectangles are similar polygons? Select each correct answer. 1)two rectangles. larger rectangle has left side labeled 1225 m and bottom labeled 144 m. the smaller rectangle has left side labeled 3.5 m and bottom side labeled 1.2 m. 2)two rectangles. larger rectangle has left side labeled 13 m and bottom labeled 5 m. the smaller rectangle has left side labeled 5.2 m and bottom side labeled 2.5 m. 3)two rectangles. larger rectangle has left side labeled 18 m and bottom labeled 6 m. the smaller rectangle has left side labeled 4.5 m and bottom side labeled 1.5 m. 4)two rectangles. larger rectangle has left side labeled 40 m and bottom labeled 15 m. the smaller rectangle has left side labeled 8 m and bottom side labeled 3 m.
Answers
Answer: Look at the picture :)
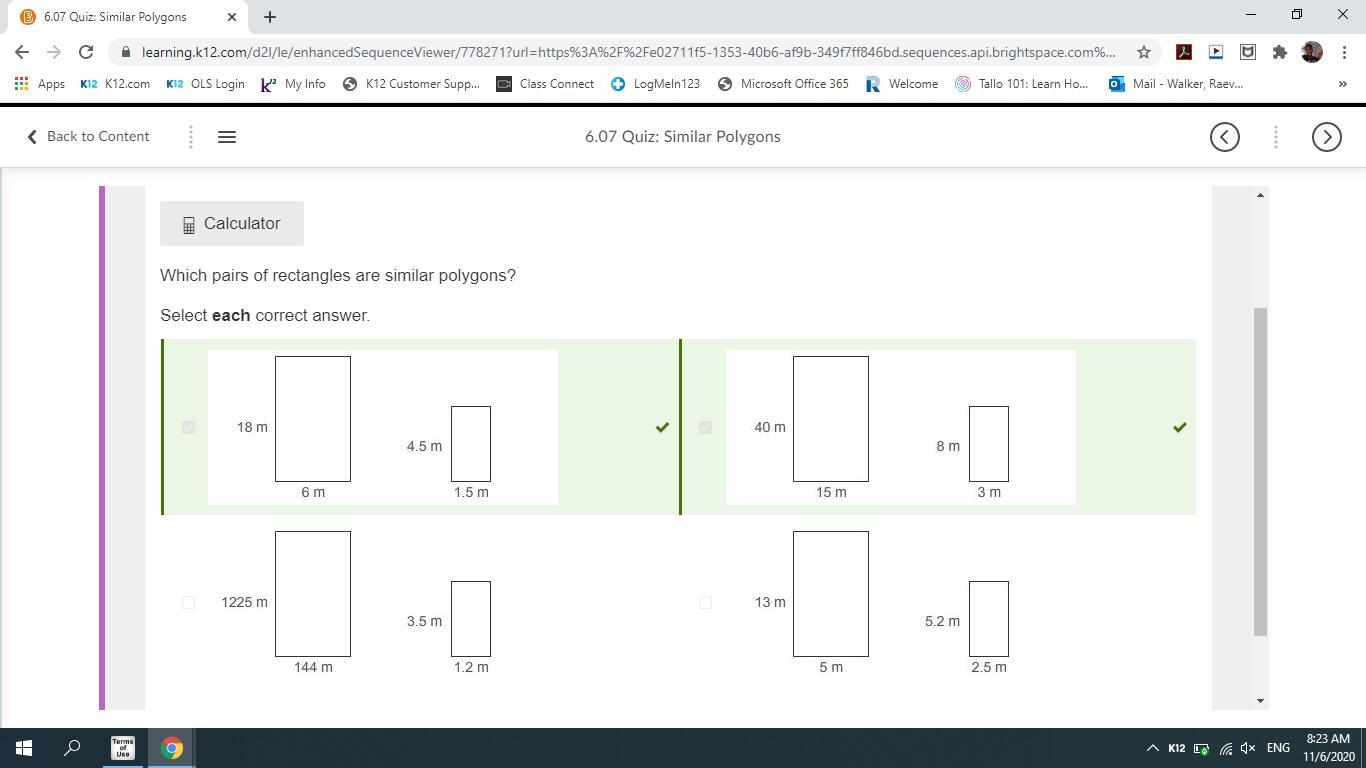
The pairs of rectangles that are similar polygons are those in;
1 and 4
For two rectangles to be similar polygons, it means that the ratio of their corresponding sides must be the same.
In question 1;
Ratio of corresponding left sides = 1225/3.5 = 350
Ratio of corresponding bottom sides = 144/1.2 = 120
Ratios do not correspond and as such they are not similar polygons.
In question 2;
Ratio of corresponding left sides = 13/5.2 = 2.5
Ratio of corresponding bottom sides = 5/2.5 = 2
Ratios do not correspond and as such they are not similar polygons.
In question 3;
Ratio of corresponding left sides = 18/4.5 = 4
Ratio of corresponding bottom sides = 6/1.5 = 2l4
Ratios correspond and as such they are similar polygons.
In question 4;
Ratio of corresponding left sides = 40/8 = 5
Ratio of corresponding bottom sides = 15/3 = 5
Ratios correspond and as such they are similar polygons.
Read more at;https://brainly.com/question/20590854
Related Questions
anyone know how to do this?
Answers
Answer:
12.1 =x
Step-by-step explanation:
Since this is a right triangle, we can use trig functions
cos theta = adj/ hyp
cos 30 = x/14
14 cos 30 = x
12.12435565 =x
12.1 =x
5196
A large rectangle is made by joining three identical small rectangles as shown.
The perimeter of one small rectangle is 21 cm.
The width of one small rectangle is x cm.
x cm
Work out the perimeter of the large rectangle.
The final line of your answer should be of the form,
Perimeter of large rectangle is ... cm
Answers
Answer:
35 cm
Step-by-step explanation:
As shown in the image attached, the A large rectangle is made by joining three identical small rectangles,
The width of one small rectangle is x cm and the length of one small rectangle is 2x cm. Therefore the perimeter of the small rectangle is given as:
2(length + width) = Perimeter
2(2x + x) = 21
2(3x) = 21
6x = 21
x = 21/6 = 3.5 cm
x = 3.5 cm
From the image attached, the width of the large rectangle is 2x (x + x) and the length is 3x (2x + x). Therefore, the perimeter of the large rectangle is:
2(length + width) = Perimeter
2(3x + 2x) = Perimeter
Perimeter = 2(5x)
Perimeter = 10x
Perimeter = 10(3.5)
Perimeter = 35 cm
Write down in terms of n, an expression for the nth term
of the following sequences:
a) 4 1 -2-5-8
b) -7 -12 -17 -22 -27
Answers
Answer:
a: -3n+1
b:-5n-2
Step-by-step explanation:
a: it is -3+1 because you can see that the sequence is going down by 3, so it is the 3 times table, but because the number is 4, and 4 is 1 more than 3, you put plus one at the end. :)
b: similar to the last, it's going down by five, but it is two less this time, so you put minus two instead.
Hope this helps :),
Lily
Find the product of (x − 3)2
Answers
Answer:
x^2-6x+9
Step-by-step explanation:
(x-3)^2
(x-3)(x-3)
x^2-3x-3x+9
x^2-6x+9
a number between 891 and 909 that is divisible by 10
Answers
Answer:
[tex]900[/tex]
Step-by-step explanation:
[tex]892/10=89.2\\893/10=89.3\\894/10=89.4\\895/10=89.5\\896/10=89.6\\897/10=89.7\\898/10=89.8\\899/10=89.9\\900/10=90\\901/10=90.1\\902/10=90.2\\903/10=90.3\\904/10=90.4\\905/10=90.5\\906/10=90.6\\907/10=90.7\\908/10=90.8\\909/10=90.9[/tex]
which of the following is the correct graph of the linear equation below? y+2=1/5(x-1)
Answers
Answer:
Step-by-step explanation:
On Monday, Crisitan groomed 15 dogs in 10 hours and Kenneth groomed 10 dogs in 8 hours. If they each make $12.75 per dog, how much did they each make on Monday?
Answers
Answer:
Christian made $191.25 and Kenneth made $127.50 each.
Step-by-step explanation:
With each dog, you multiply how many dogs with the amount of cash they get each dog.
Christian: 15x12.75= $191.25
Kenneth: 10x12.75= $127.50
So you just multiply the amount of dogs with money :)
Alejandra correctly wrote the equation y - 3 = (x - 10) to represent a line that her teacher sketched. The teacher then
changed the line so it had a slope of 2, but still went through the same point. Which equation should Alejandra write to represent
the new line?
O y-6 = 2(x - 10)
Oy-2 = 5(x - 10)
Oy-3 = {(x-2)
Oy-3 = 2(x - 10)
Answers
if y= -6 when x= -2 find y when x= 5
Answers
Answer:
Y=15 when x=5
Step-by-step explanation:
if y= -6 when x= -2
So y=? When x=5
Y=15
Hope this helps
Good Luck
Use the point-slope form of a line to write the equation of a line that has a slope of 2 and passes through the point (–4, 3). Write the equation in slope-intercept form.
Answers
Answer:
Equation of a line y = mx + c
m = slope
m = 2
Using point ( -4,3)
Equation of the line is
y - 3 = 2(x +4)
y - 3 = 2x + 8
y = 2x + 8 + 3
y = 2x + 11
Hope this helps.
Answer:
B. Y = 2x + 11
Step-by-step explanation:
Got it right on edg.
The population, P in thousands of a resort community is shown by
P(t)= 500t/2t^2+9'
where t is the time in months since city council raised property taxes.
Find the interval on which the population was 40,000 or greater
Answers
Answer:
t ≤ 4.24
Step-by-step explanation:
P(t) ≥ 40000 implies
500t/(2t²+9) ≥ 40000
Multiplying through by t², we have
500t ≥ 40000(2t²+9)
500t/40000 ≥ 2t²+9
Collecting like terms
0.0125t ≥ 2t²+9
0 ≥ 2t²+ 9 - 0.0125t
2t²+ 9 - 0.0125t ≤ 0
2t²- 0.0125t + 9 ≤ 0
Using the quadratic formula,
[tex]t = \frac{-(-0.0125) +/-\sqrt{(-.0125)^{2} - 4 X 2 X 9} }{2 X 2} \\= \frac{0.0125 +/-\sqrt{(0.00015625 - 288} }{4}\\= \frac{0.0125 +/-\sqrt{-287.9998} }{4}\\= \frac{0.0125 +/-16.97i }{4}\\=0.00313 + 4.24i or 0.00313 - 4.24i[/tex]
The factors of the equation are (t - 0.00313 -4.24i) and (t - 0.00313 + 4.24i)
So, (t - 0.00313 -4.24i)(t - 0.00313 + 4.24i) ≤ 0
(t - 0.00313)² - 4.24² ≤ 0
(t - 0.00313)² ≤ 4.24²
taking square-root of both sides,
√(t - 0.00313)² ≤ √4.24²
t - 0.00313 ≤ 4.24
t ≤ 4.24 + 0.00313
t ≤ 4.24313 ≅ 4.24
t ≤ 4.24
What is 1 + 1 in math 3
Answers
Answer:
11
Step-by-step explanation:
the answer is 11
Use completing the square to solve for X in the equation (c+7)(x-9)=25
Answers
Answer:
x = 1 ± √89
Step-by-step explanation:
Step 1: Expand
x² - 2x - 63 = 25
Step 2: Isolate xs
x² - 2x = 88
Step 3: Complete the square
x² - 2x + 1 = 88 + 1
(x - 1)² = 89
Step 3: Square root both sides
√(x - 1)² = ±√89
x - 1 = ±√89
Step 4: Isolate x
x = 1 ± √89
how do you write 25 x 10^6 in standard form
Answers
Answer:
2.5*10^7
Step-by-step explanation:
Answer:
Brainliest!!!
Step-by-step explanation:
See picture
Which point gives the vertex of f(x) = x2 – 4x + 21? Question 1 options: (–2,–17) (2,17) (–2,17) (2,–17)
Answers
Answer:
[tex](2, 17)[/tex]
Step-by-step explanation:
A parabola has the general function: [tex]f(x)=ax^2+bx+c[/tex]
In this case we have: [tex]f(x) = x^2 - 4x + 21[/tex]
where
[tex]a=1[/tex]
[tex]b=-4[/tex]
[tex]c=21[/tex]
the vertex of a parabola is in the coordinates:
[tex](\frac{-b}{2a}, \frac{-b^2+4ac}{4a} )[/tex]
substituting all of the known values, we get the following:
[tex](\frac{-(-4)}{2(1)} ,\frac{-(-4)^2+4(1)(21)}{4(1)} )\\\\(\frac{4}{2} ,\frac{-16+84}{4} )\\\\\\(2 ,\frac{68}{4} )\\\\\\(2,17)[/tex]
the vertex of [tex]f(x) = x^2 - 4x + 21[/tex] is at the point (2,17) which is the second option.
Answer:
2,17
Step-by-step explanation:
A boy carries a 2 kg bag and walks 8m on a level road to his house. How much work has he done by carrying the bag? a. 4 J b. 16 J c. zero
Answers
Answer:
160J
Step-by-step explanation:
I think this is the answer
A surveyor is 40m from the edge of a building. The angle of elevation from the surveyor to the top of the building is 55° . What is the height of the building?
Answers
Answer:
Height of building is 57.12 m.
Step-by-step explanation:
Let us try to understand the given dimensions as per the attached diagram.
Please refer to attached image (Right angled [tex]\triangle OBT[/tex])
with [tex]\angle B =90^\circ[/tex]
Let O be the point where the Surveyor is standing.
B be the point of the base of building.
T be the point of top of building.
As per question statement,
[tex]\angle O = 55^\circ[/tex]
Side OB = 40 m
To find: Side BT = ?
Using tangent trigonometric identity:
[tex]tan\theta =\dfrac{Perpendicular}{Base}[/tex]
[tex]tanO =\dfrac{BT}{BO}\\\Rightarrow tan55^\circ = \dfrac{BT}{40}\\\Rightarrow BT = tan55^\circ \times 40\\\Rightarrow BT = 1.43\times 40\\\Rightarrow BT = 57.12 m[/tex]
So, height of building is 57.12 m.
please solve
thankyou in advance x
Answers
Answer:
For the first one,
x=6 and y=16
Step-by-step explanation:
If I think of any more then I will tell you
Simplify each expression involving signed numbers.
-7 -2 = -9
12 + (-4) = 8
-8(-6) =
18/-3=
PLEASE HURRY! Thanks!
Answers
Answer:
-9=-9
8=8
-48=-48 or -8(-6)=-48
-6=-6 or 18/-3=-6
Step-by-step explanation:
Answer:
Simplify each expression involving signed numbers.
-7 – 2 =
✔ –9
12 + (-4) =
✔ 8
-8(-6) =
✔ 48
StartFraction 18 over negative 3 EndFraction =
✔ –6
can I have some brainiest
Step-by-step explanation:
Can you help me with this question
Answers
Answer:
-1.67
Step-by-step explanation:
given that £1=$1..62 what is 650 pounds in dollars
Answers
1 pound = 1.62 dollars.
Multiply total pounds by 1.62 for total dollars.
650 x 1.62 = $1,053
What is the domain of the step function f(x) = ⌈2x⌉ – 1?
Answers
Answer:
believe its 2x cause 1 was wrong
Which point is in Quadrant IV?
Answers
Answer:
1,1 or -1,3
Step-by-step explanation:
Answer:
h
Step-by-step explanation:
bottom right quadrant is IV
(8x - 4)(7y + 2) multiplying binomials
Answers
Step-by-step explanation:
8x(7y+2)-4(7y+2)
=56xy+16x-28y-8
Answer:
56xy+16x-28y-8
Step-by-step explanation:
you have to use the FOIL method to solve this is problem which is
F-First
O-Outer
I-Inner
F-Last
A ball is thrown into the air with an upward velocity of 36 ft/s. Its height h in feet after t seconds is given by the function h = –16t^2 + 36t + 10. a. In how many seconds does the ball reach its maximum height? Round to the nearest hundredth if necessary. b. What is the ball’s maximum height?
Answers
Step-by-step explanation:
We have,
A ball is thrown into the air with an upward velocity of 36 ft/s. Its height h in feet after t seconds is given by the function :
[tex]h=-16t^2 + 36t + 10[/tex] ......(1)
Part (a) :
The maximum height reached by the ball is given by :
[tex]\dfrac{dh}{dt}=0\\\\\dfrac{d(-16t^2 + 36t + 10)}{dt}=0\\\\-32t+36=0\\\\t=\dfrac{36}{32}\\\\t=1.125\ s[/tex]
Part (b) :
The maximum height of the ball is calculated by putting t = 1.125 in equation (1) such that :
[tex]h=-16(1.125)^2 + 36(1.125)+ 10\\\\h=30.25\ m[/tex]
Find the volume of this square
based pyramid.
10 in
12 in
[ ? ]
Answers
Answer:
480 in.^3
Step-by-step explanation:
volume of pyramid = (1/3) * (area of base) * height
Since this pyramid has a square for the base, the area of the base is
A = s^2, where s = length of the side of the square
volume = (1/3) * s^2 * h
volume = (1/3)(12 in.)^2 * (10 in.)
volume = (1/3)(144)(10) in.^3
volume = 480 in.^3
The volume of the square-based pyramid is 480 cubic inches as per the concept of the pyramid.
To find the volume of a square-based pyramid, we can use the formula:
Volume = (1/3) x base area x height.
In this case, the base of the pyramid is a square with a side length of 12 inches, and the height of the pyramid is 10 inches.
First, we calculate the base area of the pyramid, which is the area of the square base:
Base area = side length x side length
= 12 in x 12 in
= 144 square inches.
Now, we can substitute the values into the volume formula:
[tex]Volume = \frac{1}{3} \times 144 \times 10[/tex].
Multiplying these values, we get:
[tex]Volume = \frac{1}{3} \times1440 {in}^3[/tex]
Simplifying the expression, we have:
[tex]Volume = 480\ in^3[/tex].
To learn more about the pyramid;
https://brainly.com/question/17615619
#SPJ2
Resolve into factors:2p(p-1)-p+1
Answers
Answer:
Do it your self
Step-by-step explanation:
Hope this helps!!
Work out the surface area of this cylinder
8.2 cm
17.5 cm
Answers
Answer: 1324.12 sq. cm.
Step-by-step explanation:
A=2πrh+2πr2
A = 2π x 8.2 x 17.5 + 2π x 8.2^2
A = 2π x 143.50 + 2π x 67.24
A= 1324.12
Answer:
SA = 1324.1 cm²
Step-by-step explanation:
Surface Area of Cylinder = [tex]2\pi rh+2\pi r^2[/tex]
Where r = 8.2 cm, h = 17.5 cm
=> SA = [tex]2(3.14)(8.2)(17.5)+2(3.14)(8.2)^2[/tex]
=> SA = [tex]901.6+2(3.14)(67.24)[/tex]
=> SA = 901.6 + 422.5
=> SA = 1324.1 cm²
A company makes 140 bags.
47 of the bags have buttons but no zips.
48 of the bags have zips but no buttons.
22 of the bags have neither zips nor buttons.
A bag is selected at random.
What is the probability that the bag has buttons
Answers
Answer: 0.5
Step-by-step explanation:
Total bags (U) = 140
Number of bags with both button and zip:
(48 + 47 + x + 22) = 140
117 + x = 140
x = 140 - 117
x = 23
Therefore, probability that bag has button :
Total Number of bags with button:
(Bags with button alone + bags with both button and zip)
(47 + 23) = 70
Probability = (required outcome / Total possible outcomes)
P(bag has button) = (number of bags with button / total number of bags)
P(bag has button) = 70/140 = 0.5
P(bag has button) = 0.5
On a coordinate plane, a solid straight line has a positive slope and goes through (negative 4, 1) and (0, 3). Everything below and to the right of the line is shaded. Which linear inequality is represented by the graph? y ≤ 2x + 4 y ≤ one-halfx + 3 y ≥ One-halfx + 3 y ≥ 2x + 3
Answers
Answer: [tex]y \leq \frac{1}{2} x+3[/tex]
Step-by-step explanation:
If a function has a positive slope, that means the y value is increasing with respect to x. As you go down the x-axis, the y value will continuously increase.
First you want to plot the two sets of coords that they gave you, or else you wont know what the line looks like. Or, you could visually do it in your head. We're going down -4 on the x-axis and down 1 on the y-axis. Then for our second coords, we are going to 0 on the x-axis, then up 3 on the y-axis.
You could plot this for yourself, but im going to do it in my head for simplicity. We also need to find the slope of this function in order for us to find the y-intercept. The slope is change in y divided by the change in x. Subtract the initial position from the final position.
3 - 1 = 2
0 - (-4) = 4
2/4 = 1/2
The new equation is:
[tex]y=\frac{1}{2} x+b\\plugin(0,3)\\3=\frac{1}{2} (0)+b\\b=3[/tex]
Everything is shaded below and to the right of the line. They said the line was solid, so that means less than or equal to, [tex]\leq[/tex]
Answer:
B
Step-by-step explanation: