Answers
Answer:
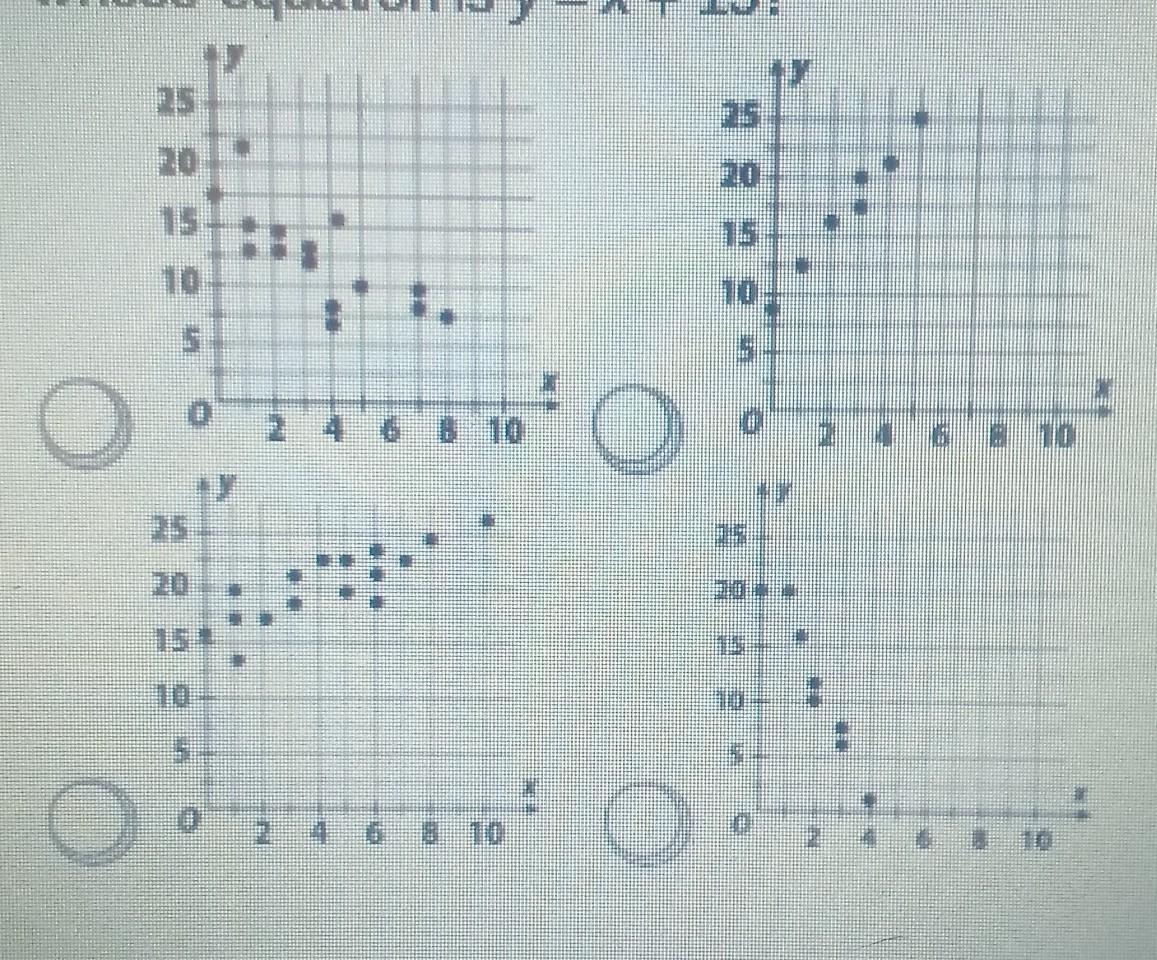
I'm going to say it's the third one (bottom left) because it's the only one that has points scattered in the same vicinity as the graph when I plugged in that equation. The line showed was linear and had many points including (0,15), (1, 16), and (2, 17).
Related Questions
The starting salaries of individuals with an MBA degree are normally distributed with a mean of $40,000 and a standard deviation of $5,000. What is the random variable in this experiment?A. Normal distribution B. $40,000 C. Starting salaries D. $5,000
Answers
Answer:
C. Starting salaries
Step-by-step explanation:
The random variable is the variable that is being descripted by the distribution. In this case, it is the variable "Starting salaries of individuals with an MBA degree".
It can take any values, but its probability is defined by the distribution and its parameter (mean and standard deviation). In theory, it could take negative values, but they would not have any validity in the real world.
The inclination (tilt) of an amusement park ride is accelerating at a rate of 2160 degreesmin22160\,\dfrac{\text{degrees}}{\text{min}^2} 2160 min 2 degrees 2160, start fraction, start text, d, e, g, r, e, e, s, end text, divided by, start text, m, i, n, end text, squared, end fraction . What is the ride's acceleration rate in degreess2\dfrac{\text{degrees}}{\text{s}^2} s 2 degrees start fraction, start text, d, e, g, r, e, e, s, end text, divided by, start text, s, end text, squared, end fraction ? degreess2\dfrac{\text{degrees}}{\text{s}^2} s 2 degrees
Answers
Answer:
um
Step-by-step explanation:
not sure sorry
Which figure is described below?
The locus of points 9 units from the
point (-1,3) on the coordinate plane.
A. circle
B. plane
C. ray
D. line
Answers
Answer:
Option A.
Step-by-step explanation:
Circle contains all points in a plane that are equidistant from a point, i.e., center of the circle.
The locus of points 9 units from the point (-1,3) on the coordinate plane.
It means, the figure represents the set of all points which are 9 units from the point (-1,3).
So, the given describes a circle with of 9 units and center at (-1,3).
Therefore, the correct option is A.
China earned a total of 70 medals at the 2016 Olympics. The number of gold medals was the same as the number of bronze medals. The number of silver medals was 8 less than the number of bronze medals. How many of each kind of medal did China earn?
Answers
Answer:ddcfs
Step-by-step explanation:
ffddcdvv
The number of the god, bronze, and silver medals are 26, 26, and 18 respectively.
What is an expression?The mathematical expression is the combination of numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also be used to denote the logical syntax's operation order and other properties.
Given that China earned a total of 70 medals at the 2016 Olympics. The number of gold medals was the same as the number of bronze medals. The number of silver medals was 8 less than the number of bronze medals.
From the given data we can form two equations as below:-
G + S + B = 70
G = B
S = B - 8
B + B - 8 + B= 70
3B = 70 + 8
B = ( 78 / 3 )
B = 26
S = 26 - 8 = 18
Therefore, the number of the god, bronze, and silver medals are 26, 26, and 18 respectively.
To know more about an expression follow
https://brainly.com/question/17332594
#SPJ2
xpress 8/(1 - 2x)2 as a power series by differentiating the equation below. What is the radius of convergence? 4 (1 - 2x) = 4(1 + 2x + 4x2 + 8x3 + ...) = 4 [infinity] Σ n=0 (2x)n SOLUTION Differentiating each side of the equation, we get 8 (1 - 2x)2 = 4(2 + Correct: Your answer is correct. + 24x2 + ...) = 4 [infinity] Σ n=1 Incorrect: Your answer is incorrect. If we wish, we can replace
Answers
Recall that for |x| < 1, we have
[tex]\dfrac1{1-x}=\displaystyle\sum_{n=0}^\infty x^n[/tex]
Replace x with 2x, multiply 4, and call this function f :
[tex]f(x)=\dfrac4{1-2x}=\displaystyle4\sum_{n=0}^\infty(2x)^n[/tex]
Take the derivative:
[tex]f'(x)=\dfrac8{(1-2x)^2}=\displaystyle8\sum_{n=0}^\infty n(2x)^{n-1}=\boxed{8\sum_{n=0}^\infty (n+1)(2x)^n}[/tex]
By the ratio test, the series converges for
[tex]\displaystyle\lim_{n\to\infty}\left|\frac{(n+2)(2x)^{n+1}}{(n+1)(2x)^n}\right|=|2x|\lim_{n\to\infty}\frac{n+2}{n+1}=|2x|<1[/tex]
or |x| < 1/2, so the radius of convergence is 1/2.
In a Local boutique you intend to buy a handbag with original price $38 a jacket with original price of 189 and a scarf with original price $23 currently the store is running a promotion for 30% off entire store in addition as a store loyalty card member you’re entitled to an extra 10% off all sales price the state charges a 5% sales tax on all purchases which is the final purchase price of the items including all discounts and sales tax write your answer to
Answers
Answer:
$165.38
Step-by-step explanation:
In the question, we are asked to work with percentages. We know that the person had bought three items of a total of 250 dollars (38 + 189 + 23). We are told that the items have a 30% discount, another 10% discount on that and a 5% tax increase on all of that.
First, let's work with the 30% discount. The official way of working out the problem you would use the unitary method. The unitary method is when we divide the total cost by 100. So 250/100, is 2.5. We multiply this by the remaining percent (100%- 30%=70%) so 2.5*70 is 175.
Then, we work with ten percent. The only difference is that instead of using the original price with are using the 30% discounted price. If we use the unitary method again we find that 175/100 is 1.75 and that multiplied by 90 (because we are only subtracting the 10% not 30%) is 157.50.
Finally, we do the same for the 5% percent only difference being we add it to 157.50. 157.50/100 is 1.575 and multiplied by 105 (because we are adding 5% onto 100% so it becomes 105%).
The final answer is 165.375 and when rounded to the nearest cent it becomes $165.38.
A Japanese garden has a circular koi pond in the middle that has a radius of 3 feet. A rectangle with length of 16 feet and width of 14 feet. A circle with radius 3 feet is cut out of the rectangle. What is the area of the Japanese garden around the koi pond? Use 3.14 for Pi. 195.74 feet squared 224.00 feet squared 252.26 feet squared 337.04 feet squared
Answers
Answer:
first, find the area of the circle cut.
r= 3 feet
π=3.14
area of a circle= πr²= 3.14×3×3= 28.26 sq.feet
Now, find the area of the rectangle and subtract it by the area of the circle.
area of rectangle = l×b
length of the rectangle= 16 feet
breadth/width of the rectangular garden= 14 feet
area= 16×14= 224 sq. feet
now, area of the garden surrounding the koi pond= 224-28.26
=195.74 sq. feet
Answer:
A. 195.74
Step-by-step explanation:
Edge2020
The given equation has been solved in the table. In which step was the subtraction property of equality applied?
Answers
Answer:
Option (D)
Step-by-step explanation:
Subtraction property of equality tells that whatever subtracted from one side of the equation must be subtracted from the other side.
If x + 2 = 2,
By the property of subtraction of equality,
x + 2 - 2 = 2 - 2
x = 0
But in the given question,
[tex]\frac{x}{2}-7=-7[/tex]
[tex]\frac{x}{2}-7+7=-7+7[/tex]
shows the addition property of equality in step (2)
Therefore, subtraction property of equality was not applied.
Option (D) will be the answer.
Two random samples with sizes 100 and n are chosen from the populations with the means 85.6 and 82.1. They have standard deviations 12.4 and 8.9, respectively. Which of these values of n would result in the smallest SE?
a. 100
b. 120
c. 90
d. 50
e. 70
Answers
Answer:
[tex] SE= \sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}[/tex]
And for this case if we have the same sample size we got the minimum value when we have the higher value fo n for each one and for this case would be the answer:
b. 120
Step-by-step explanation:
For this case we have the following info given:
[tex] n_1 = n_2 = 100[/tex]
[tex]\mu_1 = 85.6[/tex]
[tex]\mu_2 = 82.1[/tex]
[tex] \sigma_1 =12.4[/tex]
[tex]\sigma_2 = 8.9[/tex]
We assume that the variable of interest is the linear combination of the two means and for this case the standard error would be given by:
[tex] SE= \sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}[/tex]
And for this case if we have the same sample size we got the minimum value when we have the higher value fo n for each one and for this case would be the answer:
b. 120
Any percentile point for a distribution of scores must have a value equal to one of the scores.
A. True
B. False
Answers
Answer:
False.
Step-by-step explanation:
We are asked if it is true or false that any percentage point for a score distribution must have a value equal to one of the scores.
In this case we have to:
False.
Because for example, many times the median (or 50th percentile) is the mean of the inputs in middle 2, and may not equal any data point.
please simplify will give brainliyest
Answers
[tex]\displaystyle\bf\\-\sqrt{m^4n^7}=\\\\=-\sqrt{m^{2\times2}\times n^{3\times2+1}}=\\\\=-\sqrt{m^{2\times2}\times n^{3\times2}\times n}}=\\\\=-\sqrt{\Big(m^2\Big)^2\times \Big(n^3\Big)^2\times n}}=\\\\=-\sqrt{\Big(m^2\times n^3\Big)^2\times n}}=\\\\=\boxed{\bf-m^2n^3\sqrt{n}}[/tex]
What is the equation of BD, simplified?
Answers
Third option is the correct answer.
Answer:
[tex] y = \bigg[ \frac{2b}{(2a - c)} \bigg]x - \bigg[ \frac{2bc}{(2a - c)} \bigg][/tex]
Step-by-step explanation:
[tex]y - y_1 = m(x - x_1) \\ \\ y - 0 = \bigg[ \frac{2b}{(2a - c)} \bigg] (x - c) \\ \\ y = \bigg[ \frac{2b}{(2a - c)} \bigg]x - \bigg[ \frac{2b}{(2a - c)} \bigg]c \\ \\ \purple { \boxed{ \bold{y = \bigg[ \frac{2b}{(2a - c)} \bigg]x - \bigg[ \frac{2bc}{(2a - c)} \bigg]}}} \\ [/tex]
what is the y-value when x equals 30? y=350-25(x)
Answers
Answer:
-400
Step-by-step explanation:
y=350-25(x)
y=350-25x30
y=350-750
y=-400
Answer:
-400
Step-by-step explanation:
y=350-25x
x=30....
y=350-25×30
y=350-750
y=-400
At what point on the curve y = 2 + 2ex − 4x is the tangent line parallel to the line 4x − y = 3? (x, y) =
Answers
Answer:
{ln 4, (2 + 2e^ln 4 − 4 ln 4)} or (1.39, 4.45)
Step-by-step explanation:
From this equation 4x − y = 3
-y = 3 - 4x
then, y = 4x - 3
From line equation y = mx + b
Therefore, the slope is 4
Since the are parallel line, they will have same slope
Finding the derivative of y = 2 + 2e^x − 4x
y = 2 + 2e^x − 4x
y' = 0 + 2e^x - 4
Therefore,
4 = 2e^x - 4
4 = e^x
x = ln 4 = 1.39
To find the y coordinate
y = 2 + 2e^x − 4x
y = 2 + 2e^ln 4 − 4 ln 4
y = 4.45
Hence, they are parallel at point (1.39 and 4.45)
what is the y-intersept of y=4x-6
Answers
━━━━━━━☆☆━━━━━━━
▹ Answer
y-intercept = -6
▹ Step-by-Step Explanation
The format of slope is:
y = mx + b
The b represents the y-intercept which is, -6.
Hope this helps!
- CloutAnswers ❁
Brainliest is greatly appreciated!
━━━━━━━☆☆━━━━━━━
Answer: -6
Step-by-step explanation: This equation is written in slope-intercept form which is more commonly known as y = mx + b form where the multiplier or the coefficient of the x term represents the slope of the line and the b or the constant term represents the y-intercept.
So this line has a y-intercept of -6.
This means it crosses the y-axis 6 units up from origin.
the 6th term of an Arithmetic Progression is 17 and the 13th term is 38. Determine the 19th term
Answers
Answer:
56
Step-by-step explanation:
The n th term of an AP is
[tex]a_{n}[/tex] = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Given a₆ = 17 and a₁₃ = 38, then
a₁ + 5d = 17 → (1)
a₁ + 12d = 38 → (2)
Subtract (1) from (2) term by term to eliminate a₁
7d = 21 ( divide both sides by 7 )
d = 3
Substitute d = 3 into (1) and evaluate for a₁
a₁ + 5(3) = 17
a₁ + 15 = 17 ( subtract 15 from both sides )
a₁ = 2
Thus
[tex]a_{19}[/tex] = 2 + (18 × 3) = 2 + 54 = 56
Please help me and my daughter.
Answers
Answer:
you can either factorise or use tge formula method
Step-by-step explanation:
3x2−7x−20=03x2-7x-20=0
Use the quadratic formula to find the solutions.
−b±√b2−4(ac)2a-b±b2-4(ac)2a
Substitute the values a=3a=3, b=−7b=-7, and c=−20c=-20 into the quadratic formula and solve for xx.
7±√(−7)2−4⋅(3⋅−20)2⋅37±(-7)2-4⋅(3⋅-20)2⋅3
Simplify.
Tap for more steps...
x=7±176x=7±176
The final answer is the combination of both solutions.
x=4,−53
The value of the limit limx→0 sin2x/x
Answers
It is undefined.
Explanation
limx—>0 is when the value x tends to 0.
Therefore, substitute x = 0 in the expression sin2x/x.
This results in sin 2•0/0. Any value divided by 0 is undefined.
Correct me if I’m wrong please as I’m not entirely sure.
<~>\_/<~> Ho_odini <~>\_/<~>
Answer:
2Step-by-step explanation:
[tex]\bold{lim_{x\longrightarrow{0}}\dfrac{sin2x}{x}}[/tex]
[tex]\bold{lim_{x\longrightarrow{0}}\dfrac{sin2x}{x×2}×2}[/tex]
[tex]\bold{2lim_{x\longrightarrow{0}}\dfrac{sin2x}{2x}}[/tex]
[tex]\bold{2 }[/tex]PLSSSSSSSSSSSSSSSS HELP WILL MARK BRAINLIEST Ella opened a coffee shop in her neighborhood. The graph below shows the number of cups of coffee sold each hour, x, on the opening day of the coffee shop.
Answers
Answer:
The answer is B
Step-by-step explanation:
I believe this is the answer because the number starts at 0 with is the beginning.
1. Write down a pair of integers
(a) sum is -7
Answers
Answer:
-10, 3
Step-by-step explanation:
-10, 3 work since
-10 + 3 = -7
How much must be deposited today into the following account in order to have $ 50,000 in 6 years for a down payment on a house? Assume no additional deposits are made. An account with monthly compounding and an APR of 5%
Answers
Answer:
The Amount initially deposited is $37046.64
Step-by-step explanation:
A = p (1+r/n)^(nt)
A= final amount= $5000
P = principal amount=
r = rate = 0.05
n = number of times compounded
= 6*12
= 48
t = years= 6
A = p (1+r/n)^(nt)
50000 = p (1+0.05/48)^(48*6)
50000= p(1.001041667)^288
50000= p (1.34965)
50000/1.34965= p
37046.64 = p
The Amount initially deposited is $37046.64
Population of town was 21000 in 1980 and it was 20000 in 1990. Assuming the population is decreasing continuously at a rate proportion to the existing population, estimate the population in 2010.
Answers
Answer:
19,000
Step-by-step explanation:
Here, we are to estimate the population in the year 2010
From the question, we can see that within a period of a decade which is 10 years, 1000 was lost
So within the period of another decade, it is possible that another 1000 be lost
The estimated population in the year 2010 is thus 20,000 - 1,000 =
19,000
The inside diameter of a randomly selected piston ring is a randomvariable with mean value 12 cm and standard devtiation of .04cm.
a. If Xbar is the sample mean diameter form a random sample of=16 rings, where is the sampling distrbution of Xbar centered andwhat is the standard deviation of the Xbar distribution?
b. Answer the questions above for a sample of size n=64
c.find the probability that the average diameter of pistonrings from a sample size 16 is more than 11.95cm
d. For which of the above two random saples is Xbar morelikely to be within .01cm of 12cm? Explain.
Answers
Answer:
The answer is below
Step-by-step explanation:
Given that:
mean value (μ) = 12 cm and standard deviation (σ) = 0.04 cm
a) Since a random sample (n) of 16 rings is taken, therefore the mean (μx) ans standard deviation (σx) of the sample mean Xbar is given by:
[tex]\mu_x=\mu=12\ cm\\\sigma_x=\frac{\sigma}{\sqrt{n} }=\frac{0.04}{\sqrt{16} }=0.01[/tex]
The sampling distribution of Xbar is centered about 12 cm and the standard deviation of the Xbar distribution is 0.01 cm
b) Since a random sample (n) of 64 rings is taken, therefore the mean (μx) ans standard deviation (σx) of the sample mean Xbar is given by:
[tex]\mu_x=\mu=12\ cm\\\sigma_x=\frac{\sigma}{\sqrt{n} }=\frac{0.04}{\sqrt{64} }=0.005\ cm[/tex]
The sampling distribution of Xbar is centered about 12 cm and the standard deviation of the Xbar distribution is 0.005 cm
c) n = 16 and the raw score (x) = 11.95 cm
The z score equation is given by:
[tex]z=\frac{x-\mu_x}{\sigma_x} =\frac{x-\mu}{\sigma/\sqrt{n} } \\z=\frac{11.95-12}{0.04/\sqrt{16} }\\ z=-5[/tex]
P(x > 11.95 cm) = P(z > -5) = 1 - P(z < -5) = 1 - 0.000001 ≅ 1 ≅ 100%
d) for n = 64, the standard deviation is 0.01 cm, therefore it is more likely to be within .01cm of 12cm
Using the normal distribution and the central limit theorem, it is found that:
a) The sampling distribution is approximately normal, centered at 12 cm and with a standard deviation of 0.01 cm.
b) The sampling distribution is approximately normal, centered at 12 cm and with a standard deviation of 0.005 cm.
c) 100% probability that the average diameter of piston rings from a sample size 16 is more than 11.95 cm .
d) Due to the lower standard error, the sample of 64 is more likely to be within 0.01 cm of 12 cm.
In a normal distribution with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the z-score of a measure X is given by:
[tex]Z = \frac{X - \mu}{\sigma}[/tex]
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X.The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean [tex]\mu[/tex] and standard deviation [tex]s = \frac{\sigma}{\sqrt{n}}[/tex].In this problem:
Mean of 12 cm, thus [tex]\mu = 12[/tex]Standard deviation of 0.04 cm, thus [tex]\sigma = 0.04[/tex].Item a:
Sample of 16, thus [tex]n = 16[/tex] and [tex]s = \frac{0.04}{\sqrt{16}} = 0.01[/tex]
The sampling distribution is approximately normal, centered at 12 cm and with a standard deviation of 0.01 cm.
Item b:
Sample of 64, thus [tex]n = 64[/tex] and [tex]s = \frac{0.04}{\sqrt{64}} = 0.005[/tex]
The sampling distribution is approximately normal, centered at 12 cm and with a standard deviation of 0.005 cm.
Item c:
This probability is 1 subtracted by the p-value of Z when X = 11.95, thus:
[tex]Z = \frac{X - \mu}{\sigma}[/tex]
By the Central Limit Theorem:
[tex]Z = \frac{X - \mu}{s}[/tex]
[tex]Z = \frac{11.95 - 12}{0.01}[/tex]
[tex]Z = -5[/tex]
[tex]Z = -5[/tex] has a p-value of 0.
1 - 0 = 1.
100% probability that the average diameter of piston rings from a sample size 16 is more than 11.95 cm .
Item d:
Due to the lower standard error, the sample of 64 is more likely to be within 0.01 cm of 12 cm.
A similar problem is given at https://brainly.com/question/24663213
Assuming that a router that can be modeled as an M/M/1 queuing system with a mean arrival rate of 500 packets/second and a mean service rate of 1000 packets/second, what is the probability of packet loss if the number of packets in residence is limited to 10
Answers
Answer:
P(10 packet) = 0.000976
Therefore, there is a 0.000976 probability of packet loss if the number of packets in residence is limited to 10.
Step-by-step explanation:
We are given an M/M/1 queuing system
The mean arrival rate is
λ = 500 packets/second
The mean service rate is
μ = 1000 packets/second
The number of packets in residence is
n = 10
The probability of packet loss is given by
P(n packet) = ρⁿ
When n is the number of packets and ρ is the gateway utilization
The gateway utilization is given by
ρ = λ/μ
Where λ is the mean arrival rate and μ is the mean service rate.
ρ = 500/1000
ρ =0.50
So, the probability is
P(10 packet) = (0.50)¹⁰
P(10 packet) = 0.000976
Therefore, there is a 0.000976 probability of packet loss if the number of packets in residence is limited to 10.
find the common ratio of the geometric sequence: 16/3,4,3,…
Answers
Answer:
3/4
Step-by-step explanation:
r= a3/a2=3/4
or
r= a2/a1= 4÷16/3= 4×3/16= 3/4
help asap!! will get branliest.
Answers
Answer:
C
Step-by-step explanation:
A reflection is when the original diagram or picture is fliped exactly over the x axis.
HEYA!!
Answer:
Your Answer of the Question is C
if you want to prove it you can do the same thing in real life by drawing a 'W' on a paper and see its reflection on the mirror
HOPE IT MATCHES!!
Find the missing side. Round the answer to the nearest tenth. Thanks.
Answers
Answer:
74.3
Step-by-step explanation:
we can use the tangent ratio to solve for X
first, set up the equation
tan(22 deg)= 30/x
next, solve for x
multiply both sides by x
(x)(tan(22 deg))=30
then, divide both sides by tan (22 deg)
x=30/tan (22 deg)
plug this into a calculator
this gives us approximately 74.25
What is sec(5pi/3) ?? Need Help
Answers
Answer:
2
Step-by-step explanation:
When in doubt, have your calculator evaluate this.
___
The reference angle for 5π/3 is π/3. The angle is in the 4th quadrant, where the secant is positive.
sec(5π/3) = sec(π/3) = 1/cos(π/3) = 1/(1/2)
sec(5π/3) = 2
The above answer is correct! The correct answer is 2 :)
Just got it right on edge 2020!
Basic factoring. Please help!
Answers
Answer:
-1(3 - y)
Step-by-step explanation:
If you factor out a negative 1, you will get the opposite signs you already have, so -1(3 - y). To check, we can simply distribute again:
-3 + y
So our answer is 2nd Choice.
Write an equation:
For every 2 apples there
are 6 bananas
Answers
Answer:
[tex]2a=6b\\a=3b[/tex]
Step-by-step explanation:
Let [tex]a[/tex] equal the amount of apples and [tex]b[/tex] equal the amount of bananas.
[tex]2a=6b\\a=3b[/tex]
Answer:
every 2 apples there
are 6 bananas
Step-by-step explanation:
2a=6b