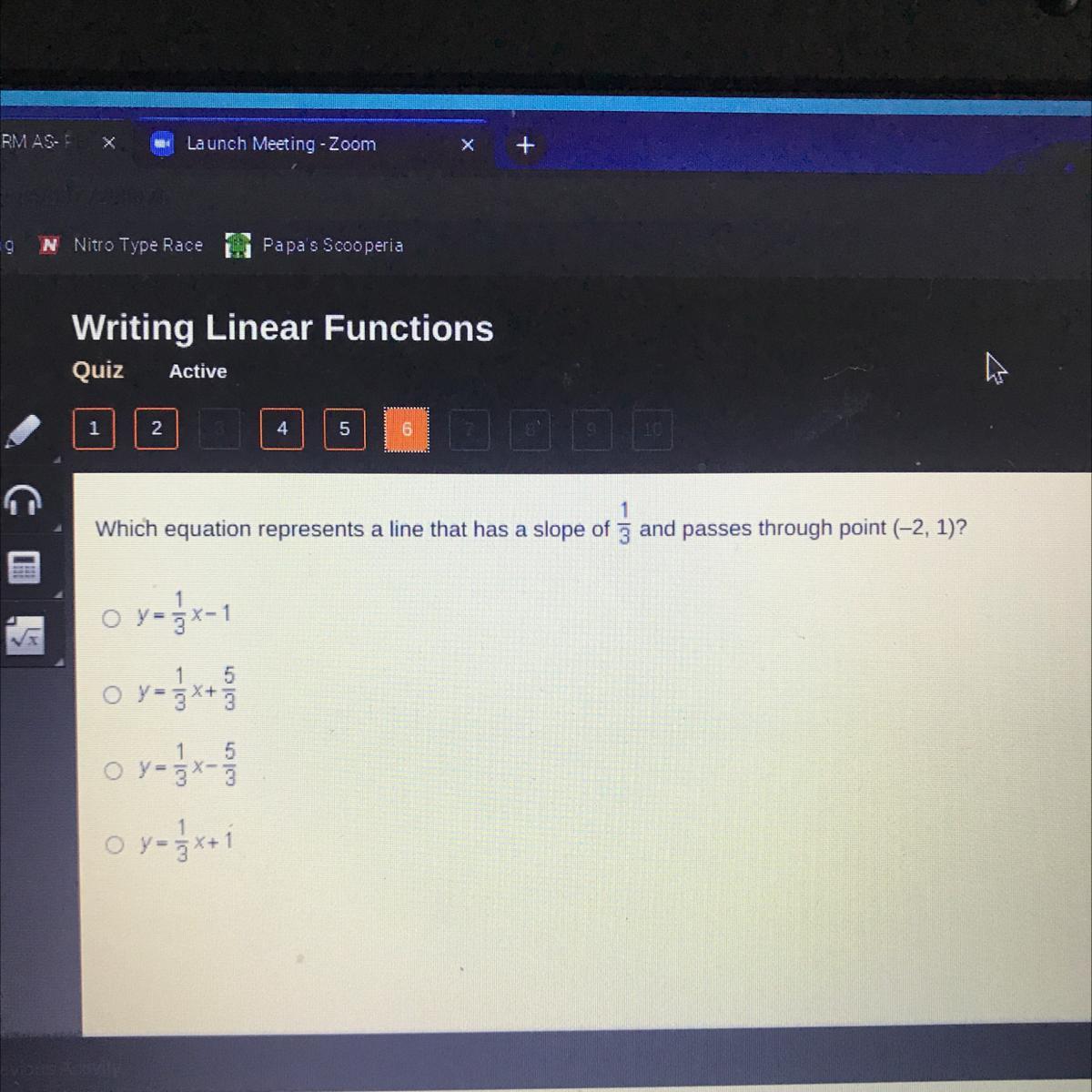
Which equation represents a line that has a slope of 1/3 and passed through point (-2,1)?

Answer:

the last one- 4/24

Step-by-step explanation:

ive answered this question before and got it correct

Answer:

In 59 days, the number of bacteria reaches 1000.

Step-by-step explanation:

 Given the data in the question;

by placing 100 spores of the bacteria at the start of the project,

p(0) = 100

dP over dt equals the product of 0.05 times P and the quantity 1 minus P over 2000

dp/dt = 0.05p( 1 - p/200 )

2000dp / p( 2000 - p ) = 0.05dt

[1 / p + 1 / 200-p ]dp = 0.05 dt

Now, we integrate

∫[1 / p + 1 / 200-p ]dp = ∫ 0.05 dt

ln p - ln [2000 - p ]  = 0.05 + c'

ln[ p / 2000 - p ] = 0.05 + c'

p / 2000 - p  = [tex]e^{0.05t + c'[/tex]

p / 2000 - p  = k[tex]e^{0.05t[/tex]

Now, since p(0) = 100, we substitute

100 / (2000 - 100)  = k[tex]e^{0.05(0)[/tex]

100 / 1900  = k × [tex]e^{0[/tex]

100 / 1900  = k × 1

k = 1 / 19

Therefore,

p / 2000 - p  = k[tex]e^{0.05t[/tex]

p / 2000 - p  = (1/19)[tex]e^{0.05t[/tex]

when p( t ) = 1000, then t will be;

1000 / (2000 - 1000)  = (1/19)[tex]e^{0.05t[/tex]

1000 / 1000  = (1/19)[tex]e^{0.05t[/tex]

1  = (1/19 ) × [tex]e^{0.05t[/tex]

1/(1/19 )  = [tex]e^{0.05t[/tex]

(1 × 19)/1 = [tex]e^{0.05t[/tex]

[tex]e^{0.05t[/tex] = 19

0.05t = ln( 19 )

0.05t = 2.9444

t = 2.9444 / 0.05

t = 58.888 ≈ 59 days

Therefore, In 59 days, the number of bacteria reaches 1000.

Answer:

The answer is 120

Step-by-step explanation:

5! = 120

Thus, The answer is 120

-TheUnknownScientist

Answer:

Speed= 0.6666667 miles per hour

Step-by-step explanation:

You can find the average speed of an object if you know the distance traveled and the time it took. The formula for speed is speed = distance ÷ time. To work out what the units are for speed, you need to know the units for distance and time.

Answer:

5.5

Step-by-step explanation:

5 + 6 =

11 / 2 =

5.5

Answer:

Area of three triangles = 36 square units

Area of the composite figure = 60 square units

Step-by-step explanation:

Area of a triangle = [tex]\frac{1}{2}(\text{Base})(\text{Height})[/tex]

Area of ΔABC = [tex]\frac{1}{2}(6)(4)[/tex]

                        = 12 square units

Area of ΔCDE = [tex]\frac{1}{2}(4)(6)[/tex]

                        = 12 square units

Area of ΔGEF = [tex]\frac{1}{2}(6)(4)[/tex]

                       = 12 square units

Area of rectangle ACEG = Length × Width

                                        = AC × CE

                                        = 6 × 4

                                        = 24 square units

Area of three triangles = 12 + 12 + 12

                                      = 36 square units

Area of the composite figure = Area of three triangles + Area of the rectangle

= 36 + 24

= 60 square units

Answer:

The total area of the three triangles is 36 square units.

The area of the figure is 60 square units.

Step-by-step explanation:

Answer:

D. [tex] y - y_0 = m(x - x_0) [/tex].

Step-by-step explanation:

The equation of a line can be written in the point-slope form if we know the the coordinates of a point the line passes through which is [tex] (x_0, y_0) [/tex]. And if we also know the slope = m of the line.

Therefore, the point-slope equation is given as:

[tex] y - y_0 = m(x - x_0) [/tex]

Answer:

1288 c m 3

Step-by-step explanation:

To work out volume, you just do the simple calculation of height x width x length. So what we need to do here is 6 x 7.5 x 22.9 =  

1212.5 c m 3  .

The decimal is a 5 so that is rounded up to give the nearest meter hence the answer to the question is  

1288 c m 3  .

Answer:

your answere is 80 degrees

Step-by-step explanation:

the total of the inside is 180 so subtract 35 and 65 from 180 and you get 80

Answer:

I don't know this sorry

Answer:

the photos unclear if you take another and post it I can answer it

Step-by-step explanation:

Answer:

Horizontal: if y is equal to 0, then there is no vertical movement

Answer:

a)

We know that:

a, b > 0

a < b

With this, we want to prove that a^2 < b^2

Well, we start with:

a < b

If we multiply both sides by a, we get:

a*a < b*a

a^2 < b*a

now let's go back to the initial inequality.

a < b

if we now multiply both sides by b, we get:

a*b < b*b

a*b < b^2

Then we have the two inequalities:

a^2 < b*a

a*b < b^2

a*b = b*a

Then we can rewrite this as:

a^2 < b*a < b^2

This means that:

a^2 < b^2

b) Now we know that a.b > 0, and a^2 < b^2

With this, we want to prove that a < b

So let's start with:

a^2 < b^2

only with this, we can know that a*b will be between these two numbers.

Then:

a^2 < a*b < b^2

Now just divide all the sides by a or b.

if we divide all of them by a, we get:

a^2/a < a*b/a < b^2/a

a < b < b^2/a

In the first part, we have a < b, this is what we wanted to get.

Another way can be:

a^2 < b^2

divide both sides by a^2

1 < b^2/a^2

Let's apply the square root in both sides:

√1 < √( b^2/a^2)

1 < b/a

Now we multiply both sides by a:

a < b

Answer

The area is 54cm² To get the area i split the shape into two shape both having a length of 9in and a width of 3in. I calculate the area for one by using lxw=area and get 27 and times that by two to get 54.

When calculating the area for this object you get 54 and you add the ²symbol because its area is not one dimensioned it is two dimensioned or length times width not just length, so you use the ² symbol to show that.

Answer:

the answer is

b.)42cm2

Step-by-step explanation:

if u add all the figures together u will get ur answer

Answer:

15.3

Step-by-step explanation:

Cos 32 = x/18

Cos 32 = 0.848048096

x/18 = 0.848048096

x = 15.3 (rounded)

Answer:

8 feet

Step-by-step explanation:

Volume = length * width * height

Substitute the values.

288 = 9 * 4 * height

Divide both sides by 36

height = 288/36

height = 8 feet

Answer:

[tex]\text{Area}=\frac{15(x+1)}{2(x-2)}[/tex]

Step-by-step explanation:

Length of the rectangle given in the picture = [tex]\frac{5x+5}{x+3}[/tex]

Width of the rectangle = [tex]\frac{3x+9}{2x-4}[/tex]

Area of the rectangle = Length × Width

                                    = [tex]\frac{5x+5}{x+3}\times \frac{3x+9}{2x-4}[/tex]

                                    = [tex]\frac{5(x+1)}{x+3}\times \frac{3(x+3)}{2(x-2)}[/tex]

                                    = [tex]\frac{15(x+1)(x+3)}{2(x+3)(x-2)}[/tex]

                                    = [tex]\frac{15(x+1)}{2(x-2)}[/tex]

Therefore, area of the given rectangle is [tex]\frac{15(x+1)}{2(x-2)}[/tex].

Answer:

a

Step-by-step explanation:

please make me Brianlist please

Answer:

[tex]16^2-(\dfrac{x}{2})^2=(16+\dfrac{x}{2})(16-\dfrac{x}{2})[/tex]

Step-by-step explanation:

The given expression is : [tex]256-\dfrac{x^2}{4}[/tex].

We need to factorize it.

We know that, 16² = 256

So,

[tex]256-\dfrac{x^2}{4}=(16)^2-(\dfrac{x}{2})^2[/tex]

We know that, [tex]a^2-b^2=(a-b)(a+b)[/tex]

[tex]16^2-(\dfrac{x}{2})^2=(16+\dfrac{x}{2})(16-\dfrac{x}{2})[/tex]

Hence, this is the required solution.

Answer:

Step-by-step explanation:

they get 4%  or 4 out of ever 100.  that's 25 for one AB donation.

The equation of the ellipse with foci at (0 ±10) and vertices at (0 ±11) is [tex]\frac{x^2}{21} + \frac{y^2}{100} = 1[/tex]

We have:

Vertices = (0, ± 11),

Foci = (0, ± 10)

The vertices and the foci are represented as:

Foci = (0, ± a)

Vertices = (0, ± c)

So, we have:

a = 10

c = 11

The equation of b is calculated using:

b² = c²- a²

So, we have:

b² = 11²- 10²

Evaluate

b² = 21

The equation of the ellipse is then represented as:

[tex]\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1[/tex]

This gives

[tex]\frac{x^2}{21} + \frac{y^2}{10^2} = 1[/tex]

[tex]\frac{x^2}{21} + \frac{y^2}{100} = 1[/tex]

Hence, the equation of the ellipse is [tex]\frac{x^2}{21} + \frac{y^2}{100} = 1[/tex]

Read more about ellipse equations at:

https://brainly.com/question/10411406

#SPJ2

Answer:

x^2/221+Y^2/121=1

Step-by-step explanation:

If y = y(x), then the slope of the tangent line to (1, 1) is equal to the value of the derivative dy/dx when x = 1 and y = 1.

Compute the derivative using implicit differentiation:

d/dx [xy ^2 + y] = d/dx [2x]

d/dx [xy ^2] + d/dx [y] = 2 d/dx [x]

(x d/dx [y ^2] + d/dx [x] y ^2) + dy/dx = 2

2xy dy/dx + y ^2 + dy/dx = 2

(2xy + 1) dy/dx = 2 - y ^2

dy/dx = (2 - y ^2) / (2xy + 1)

Plug in x = 1 and y = 1 :

slope = dy/dx = (2 - 1^2) / (2*1*1 + 1) = 1/3

Now use the point-slope formula to get the equation of the line:

y - 1 = 1/3 (x - 1)

y = x/3 + 2/3

Answer: You use it to represent that the equation your graphing is either greater than or equal too or less than or equal too

Step-by-step explanation:

A dotted line is there to represent that the equation your graphing is either grater than or less than

So the solid line represents the same thing, except that they both have a possibility of being equal too which is why the line is solid.

I hope this helps!

Answer:

Step-by-step explanation:

i dont know sorry

Answer:

a) section c

b) at a constant rate

c) below

A. 3m/s^2

B. 0 m/s^2

C. -3m/s^2

D. 1 m/s^2

Step-by-step explanation:

a) This graph models the change in velocity of time. Since when the velocity decreases over time, the acceleration is negative. This relationship is modeled in the interval from the 9th to 11th seconds which is section c.

b) If the graph is flat, it means the car is traveling at the same amount of meters per second. This means the car is traveling at a constant rate during section b.

c) During section A, the velocity in second 0 to second 4 increases by 12m/s. So, the acceleration is 3m/s^2. This is identical to finding the slope.

During section B, the velocity does not change at all, so the acceleration(and slope) is 0 m/s^2

During section C, over 2 seconds, from 9 to 11, the velocity goes from 12 m/s to 6 m/s, which is a change of -6 m/s. Therefore, the acceleration is -3m/s^2

During section D, over a span of 4 seconds(11 - 15), the velocity changes from 6 m/s to 10 m/s. That means a change of 4 m/s and the acceleration would be 1 m/s^2.

Answer:

A=44yd²

Step-by-step explanation:

Answer: The rates of change for both function A and function B are positive : TRUE

The rates of change for functions A is 3 times the rate of change for function B : FALSE

The y - intercepts for both Function A and Function B are positive : FALSE

Step-by-step explanation:

Answer:

C. The height of the tide 30 hours after the original observation is 8 feet.

Step-by-step explanation:

I calculated it logically

Answer:

240 inches squared

Step-by-step explanation:

12 x ( 3 + 17) =

12 x 20 =

240 inches squared

Answer:

A. -21

Step-by-step explanation:

y varies directly as x

y = kx

----------------------

y = 15 when x = -5

Find k, the constant of variation

15 = k(-5)

Divide both sides by -5

-3 = k

k = -3

------------------------------

y when x= 7

using k = -3

y = -3(7)

y = -21