Answers
Step-by-step explanation:
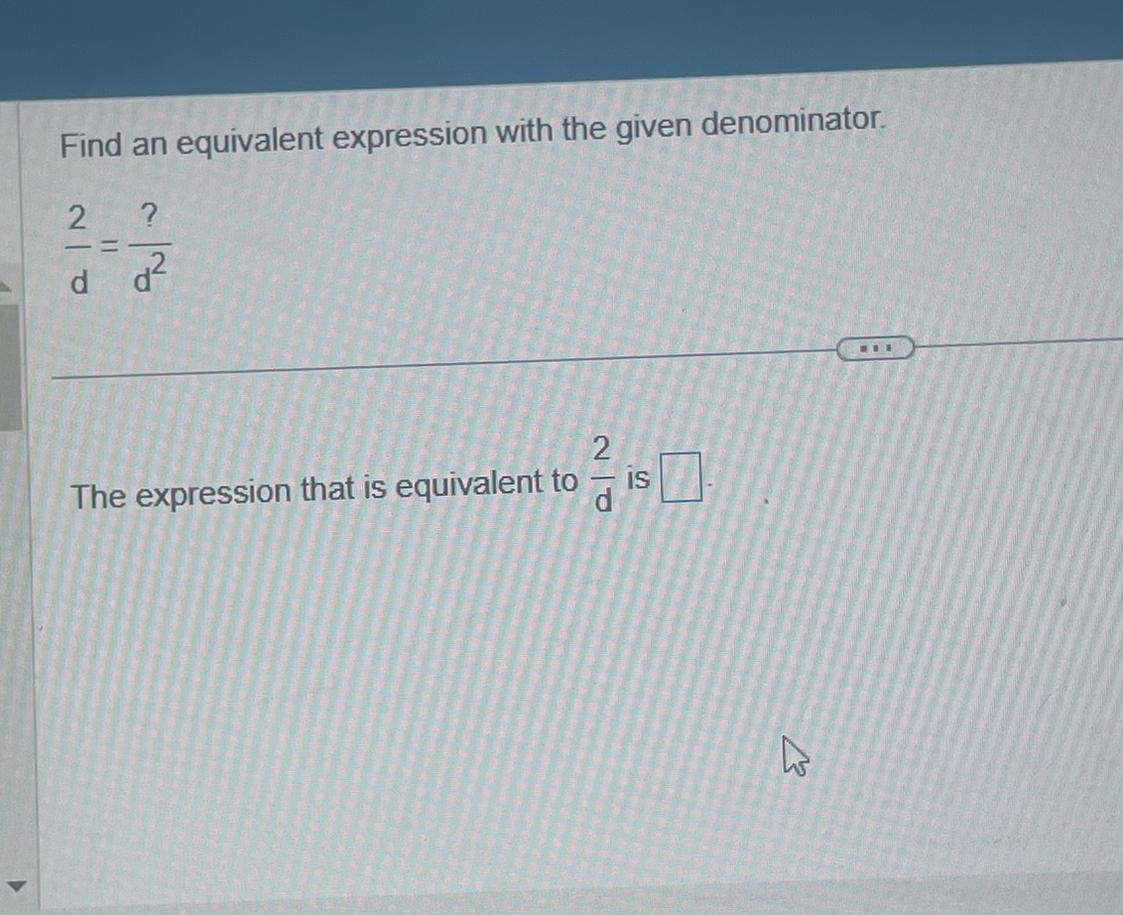
Multiply the L side of the equation by d/d ( this is just multiplying by 'one' )
2/d * d/d = 2d / d^2
Related Questions
6 in.
3.2 in.
2 in.
3.2 in.
1 in.
square inches
1 in.
The container will be made from cardboard. How many
square inches of cardboard are needed to make one
container? Assume there are no overlapping areas.
Answers
The square inches of cardboard paper used is 56.8 square inches
Calculating the square inches of cardboard paperFrom the question, we have the following parameters that can be used in our computation:
The prism
The square inches of cardboard paper is the surface area of the pyramid
And this is calculated as
Area = bh + L(Sum of side lengths)
Using the above as a guide, we have the following:
Area = 2 * 3.2 + 6 * (2 + 3.2 + 3.2)
Evaluate
Area = 56.8
Hence, the square inches of construction paper used to make the container is 56.8 square inches
Read more about surface area at
brainly.com/question/26403859
#SPJ1
Match each system on the left with all words that describe the system on the right. Choices on the right can be used more than once. y = 3x - 1 2y - 6x = 4 2y = -x + 6 4y + 2x = 12 y = 2x + 3 x+y = -9 inconsistent consistent independent dependent
Answers
y = 3x - 1: consistent, independent
2y - 6x = 4: consistent, independent
2y = -x + 6: consistent, independent
4y + 2x = 12: consistent, independent
y = 2x + 3: consistent, independent
x + y = -9: consistent, dependent
y = 3x - 1 and 2y = -x + 6: inconsistent
Let's match each system on the left with the appropriate words that describe the system on the right:
y = 3x - 1: consistent, independent
This system represents a linear equation with a unique solution. The equations are not multiples of each other, and they intersect at a single point.
2y - 6x = 4: consistent, independent
Similar to the first system, this represents a linear equation with a unique solution. The equations are not multiples of each other, and they intersect at a single point.
2y = -x + 6: consistent, independent
This system also represents a linear equation with a unique solution. The equations are not multiples of each other, and they intersect at a single point.
4y + 2x = 12: consistent, independent
Like the previous systems, this represents a linear equation with a unique solution. The equations are not multiples of each other, and they intersect at a single point.
y = 2x + 3: consistent, independent
This system represents a linear equation with a unique solution. The equations are not multiples of each other, and they intersect at a single point.
x + y = -9: consistent, dependent
This system represents a linear equation with infinitely many solutions. The equations are multiples of each other, meaning they represent the same line. Therefore, any point on the line satisfies both equations.
y = 3x - 1 and 2y = -x + 6: inconsistent
This system represents inconsistent equations that do not have a common solution. The lines represented by the equations are parallel and do not intersect.
To summarize the matches:
y = 3x - 1: consistent, independent
2y - 6x = 4: consistent, independent
2y = -x + 6: consistent, independent
4y + 2x = 12: consistent, independent
y = 2x + 3: consistent, independent
x + y = -9: consistent, dependent
y = 3x - 1 and 2y = -x + 6: inconsistent
for such more question on consistent
https://brainly.com/question/17448505
#SPJ8
John, Rick, and Molli can paint a room working together in 5 hours. Alone, Molli can paint the room in 14 hours. If Rick works alone, he can paint the room in 10 hours. Write an equation comparing the group rate to the sum of the individual rates. Then find how long it will take John to paint the room if working alone.
Answers
It will take John approximately 2.69 hours to paint the room alone.
Let's denote the individual rates of John, Rick, and Molli as J, R, and M, respectively. We are given the following information:
John, Rick, and Molli can paint the room together in 5 hours.
Molli alone can paint the room in 14 hours.
Rick alone can paint the room in 10 hours.
To find the equation comparing the group rate to the sum of the individual rates, we can use the concept of work done. The amount of work required to paint the room is the same, regardless of who is doing the work.
The equation can be expressed as:
1/5 = 1/J + 1/R + 1/M
Now, let's substitute the given information into the equation. We know that:
M = 14 (since Molli can paint the room alone in 14 hours)
R = 10 (since Rick can paint the room alone in 10 hours)
Substituting these values, the equation becomes:
1/5 = 1/J + 1/10 + 1/14
To solve for J, we can find the least common denominator (LCD) of 10 and 14, which is 70:
14J + 7J + 5J = 70
26J = 70
J = 70/26
J ≈ 2.69
Therefore, it will take John approximately 2.69 hours to paint the room alone.
for such more question on hours
https://brainly.com/question/23377525
#SPJ8
Factorize
8(p-q)^3-(p+q)^3
Answers
The factorization of[tex]8(p-q)^3-(p+q)^3 is 8(p-q)^3 - (p+q)^3 is [p - 3q][7p^2 - 8pq + 3q^2].[/tex]
The given expression is[tex]8(p-q)^{3}-(p-q)^{3}[/tex]
To factorize this expression, we can use the identity for the difference of cubes, which states that [tex]a^3 - b^3 = (a - b)(a^2 + ab + b^2).[/tex]
Let's apply this identity to the given expression:
[tex]8(p-q)^3 - (p+q)^3 = [2(p-q)]^3 - (p+q)^3.[/tex]
Now we can see that we have a difference of cubes:[tex](2(p-q))^3 - (p+q)^3.[/tex]
Using the identity, we can factorize this expression as follows:
[tex][(2(p-q)) - (p+q)][(2(p-q))^2 + (2(p-q))(p+q) + (p+q)^2].[/tex]
Simplifying further:
[tex][2p - 2q - p - q][(2(p-q))^2 + (2(p-q))(p+q) + (p+q)^2].[/tex]
Combining like terms:
[tex][p - 3q][(2(p-q))^2 + 2(p-q)(p+q) + (p+q)^2].[/tex]
Expanding the squared term:
[tex][p - 3q][4(p^2 - 2pq + q^2) + 2(p^2 - q^2) + (p^2 + 2pq + q^2)].[/tex]
Simplifying:
[tex][p - 3q][4p^2 - 8pq + 4q^2 + 2p^2 - 2q^2 + p^2 + 2pq + q^2].[/tex]
Combining like terms again:
[tex][p - 3q][7p^2 - 8pq + 3q^2].[/tex]
Therefore, the factorization of [tex]8(p-q)^3 - (p+q)^3 is [p - 3q][7p^2 - 8pq + 3q^2].[/tex]
For more such questions on factorization, click on:
https://brainly.com/question/18187355
#SPJ8
At Bud's company, bowling balls are shaped as a sphere with a diameter of 12 inches. If a store receives a shipment of 21 bowling balls, what is the total volume of the balls? (Use 3.14 for pi)
Answers
The total volume of the 21 bowling balls is 6048π cubic inches.
We have,
To find the total volume of the 21 bowling balls, we first need to calculate the volume of a single ball and then multiply it by the number of balls.
The volume of a sphere can be calculated using the formula:
V = (4/3) x π x r³
where V is the volume and r is the radius of the sphere.
Given that the diameter of the bowling ball is 12 inches, the radius can be calculated as half of the diameter:
r = 12/2 = 6 inches
Now we can calculate the volume of a single ball:
V_ball = (4/3) x π x (6³) = (4/3) x π x 216 = 288π cubic inches
Since there are 21 balls, we can calculate the total volume by multiplying the volume of a single ball by the number of balls:
Total volume = 21 x 288π = 6048π cubic inches
Thus,
The total volume of the 21 bowling balls is 6048π cubic inches.
Learn more about Sphere here:
https://brainly.com/question/12390313
#SPJ1
find the quotient : 6x/(3x+15) divided by (x^2+2x)/ (x^2+7x+10)
Answers
The quotient of[tex](6x/(3x+15)) / ((x^2+2x)/ (x^2+7x+10))[/tex] is 2x.
To simplify the expression[tex](6x/(3x+15)) / ((x^2+2x)/ (x^2+7x+10)),[/tex] we can use the rule for dividing fractions, which states that dividing by a fraction is the same as multiplying by its reciprocal.
Let's simplify the expression :
Simplify the numerator and denominator of the first fraction.
The numerator is 6x, and the denominator is (3x+15).
We can factor out a common factor of 3 from the denominator, which gives us 3(x+5).
So the first fraction simplifies to 6x / 3(x+5).
Simplify the numerator and denominator of the second fraction.
The numerator is (x^2+2x), and the denominator is [tex](x^2+7x+10).[/tex]
We can factor both the numerator and denominator:
Numerator: x(x+2)
Denominator: (x+5)(x+2)
Canceling out the common factor of (x+2), we are left with x / (x+5).
Multiply the two simplified fractions.
Multiplying the fractions, we get:
[tex](6x / 3(x+5)) \times (x / (x+5))[/tex]
Simplify the resulting expression.
Canceling out the common factor of (x+5) in the numerator and denominator, we are left with:
2x / 1
So the quotient simplifies to 2x.
Therefore, the quotient of [tex](6x/(3x+15)) / ((x^2+2x)/ (x^2+7x+10))[/tex] is 2x.
For similar question on quotient.
https://brainly.com/question/11418015
#SPJ8
pls help and show work
Answers
Hence the surface area of the given figure 168 km².
In the given prism contains
3 rectangular surface,
For rectangular surface 1:
Length = 6 km
Width = 7 km
Surface area = 6x7
= 42 km²
For rectangular surface 2:
Length = 8 km
Width = 7 km
Surface area = 8x7
= 56 km²
For rectangular surface 3:
Length = 10 km
Width = 7 km
Surface area = 10x7
= 70 km²
Hence total surface area of the given figure is,
⇒ 42 + 56 + 70
⇒ 168 km²
To learn more about prism visit:
https://brainly.com/question/2918181
#SPJ1
the ratio of women to men in a local book club is 7 to 3. whitch combanation of women to the total could the club have
Answers
The possible combinations of women to the total number of club members could be:
7 women out of 10 members.
14 women out of 20 members.
21 women out of 30 members.
28 women out of 40 members.
And so on, as long as "x" is a multiple of 10 that is divisible by 7.
The ratio of women to men in the local book club is 7 to 3. This means that for every 7 women, there are 3 men.
To find the possible combinations of women to the total number of club members, we can consider the total number of members as a multiple of 10 (since the ratio is given as 7 to 3). Let's assume the total number of club members is represented by the variable "x."
Based on the given ratio, we can calculate the number of women in terms of "x" by multiplying the ratio of women (7/10) by the total number of members:
Number of women = (7/10) * x
Since we're looking for possible combinations, the number of women must be a whole number. Therefore, "x" must be a multiple of 10 that is divisible by 7.
Let's explore some possible combinations:
If x = 10, the number of women = (7/10) * 10 = 7, which satisfies the ratio.
If x = 20, the number of women = (7/10) * 20 = 14, which satisfies the ratio.
If x = 30, the number of women = (7/10) * 30 = 21, which satisfies the ratio.
If x = 40, the number of women = (7/10) * 40 = 28, which satisfies the ratio.
As you can see, the possible combinations of women to the total number of club members could be:
7 women out of 10 members.
14 women out of 20 members.
21 women out of 30 members.
28 women out of 40 members.
And so on, as long as "x" is a multiple of 10 that is divisible by 7.
For such more questions on Ratio of Women:Men
https://brainly.com/question/15252151
#SPJ8
How many real and complex roots exist for the polynomial
F(x)= x³ +2x² + 4x+8 ?
OA. 2 real roots and 1 complex root
OB. 1 real root and 2 complex roots
C. 3 real roots and 0 complex roots
D. 0 real roots and 3 complex roots
Answers
The roots of the function F(x) = x³ + 2x² + 4x + 8 are given as follows:
B. 1 real root and 2 complex roots.
How to identify the zeros of the function?The function in this problem is defined as follows:
F(x) = x³ + 2x² + 4x + 8.
The function is of the third degree, hence the total number of zeros of the function is of 3.
From the graph, the function has only one x-intercept, which is given as follows:
x = -2.
Hence the two remaining roots are the complex roots, meaning that option B is the correct option for this problem.
More can be learned about the zeros of a function at brainly.com/question/16550963
#SPJ1
I cant seem to understand this question and i need the answer really quick.
Answers
The person will need approximately 28 square yards of material for the tent.
To calculate the amount of material needed, we first need to determine the total surface area of the tent.
The tent has six sides: a top, a bottom, a front, a back, and two sides. The top and bottom are both 10 feet by 5 feet, so their combined area is 10 feet x 5 feet = 50 square feet each.
The front and back are both 10 feet by 5 feet, so their combined area is also 10 feet x 5 feet = 50 square feet each.
The two sides are both 5 feet by 5 feet, so their combined area is 5 feet x 5 feet = 25 square feet each.
To find the total surface area, we add up all these areas:
Top and bottom: 50 square feet + 50 square feet = 100 square feet
Front and back: 50 square feet + 50 square feet = 100 square feet
Sides: 25 square feet + 25 square feet = 50 square feet
Total surface area: 100 square feet (top and bottom) + 100 square feet (front and back) + 50 square feet (sides) = 250 square feet
Since the material is sold in square yards, we need to convert square feet to square yards.
There are 9 square feet in 1 square yard.
So, 250 square feet / 9 = 27.78 square yards.
Rounding up to the nearest square yard, the person will need approximately 28 square yards of material for the tent.
Learn more about total surface area click;
https://brainly.com/question/15476071
#SPJ1
When solving a linear system of equations, you are looking for which of the following?
Answers
When solving a linear system of equations, you are looking for the points of intersection between the equations
How to determine the statement that completes the given statementFrom the question, we have the following parameters that can be used in our computation:
Solving a system of linear equations
Also, we have the following from the options
Slopey-interceptx-interceptPoints of intersectionThe general rile is that
Slope = rate of change
x and y intercepts = when y and x equals 0
points of intersection = solution to the system
Hence, you are looking for the points of intersection between the equations
Read more about equations at
https://brainly.com/question/148035
#SPJ1
Question
When solving a linear system of equations, you are looking for which of the following?
Slope
y-intercept
x-intercept
Points of intersection
Please Help!! Solve For X
Answers
The value of x in the given figure is 8.
In the given figure there are two lines which are parallel.
We have to find the value of x.
In the straight line the sum of angles is 180 degrees.
8x+1+115=180
8x+116=180
Subtract 116 from both sides:
8x=180-116
8x=64
Divide both sides by 8:
x=64/8
x=8
Hence, the value of x in the given figure is 8.
To learn more on Angles click:
https://brainly.com/question/28451077
#SPJ1
While driving your rental car on your vacation in Europe, you find that you are getting 13.3 km/of gasolineWhat does this value correspond to in miles per gallon?
13.3km/L=__________mi/gal
Answers
The rental car is getting approximately 37.56 miles per gallon.
To convert kilometers per liter (km/l) to miles per gallon (mpg), you can use the following conversion factor:
1 km/l ≈ 2.82475 mpg
Therefore, if your rental car is getting 13.3 km/l of gasoline, the equivalent value in miles per gallon would be:
13.3 km/l x 2.82475 mpg ≈ 37.56 mpg
So, your rental car is getting approximately 37.56 miles per gallon.
Learn more about conversion factor click;
https://brainly.com/question/30567263
#SPJ1
arrange the numbers: -7 -5 -3 3 -1 1 into three pairs with the same total
Answers
The numbers -7, -5, -3, 3, -1, and 1 can be arranged into three pairs with the same total (-7, 7), (-5, 5), (-3, 3), (-1, 1).
To arrange the numbers -7, -5, -3, 3, -1, and 1 into three pairs with the same total, we need to find a combination of pairs that will give us the same sum for each pair.
Let's start by examining the numbers:
-7, -5, -3, 3, -1, 1
To find pairs with the same total, we can start by pairing the numbers with their additive inverses (numbers that sum to zero). In this case, -7 and 7, -5 and 5, -3 and 3 can be paired up. This leaves us with -1 and 1.
We have three pairs now: (-7, 7), (-5, 5), (-3, 3). However, we still have -1 and 1 remaining. To make the sum of the pairs equal, we can pair -1 with 7 and 1 with -5.
The three pairs with the same total are:
(-7, 7), (-5, 5), (-3, 3), (-1, 1).
Each pair sums up to zero, resulting in the same total for each pair. For example, (-7 + 7 = 0), (-5 + 5 = 0), and so on.
Therefore, the numbers -7, -5, -3, 3, -1, and 1 can be arranged into three pairs with the same total:
(-7, 7), (-5, 5), (-3, 3), (-1, 1).
For more question on pairs visit:
https://brainly.com/question/30508892
#SPJ8
If A={o,b,s,e,r,v,a,n,t,l,y} and U={a,b,c,d,e,f,g,h,I,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z} find [A’]
Answers
Answer:
[A'] = {c,d,f,g,h,i,j,k,m,n,p,q,u,w,x,z}
Step-by-step explanation:
[A'] is read as the set of A complement, which is all the elements from the universal set that are not contained in set A.
Therefore, [A'] = {c,d,f,g,h,i,j,k,m,n,p,q,u,w,x,z}
Burning Brownie has five varieties of cakes as Chocolate fudge cake (Cake 1), Nutella-filled Cake (Cake 2), Marble Cake (Cake 3), Cheese cake (Cake 4) and Fruit Cake (Cake 5) at their store. The selling prices of each of the cakes are $9, $12, $4, $5, $8 respectively. a. Formulate the Revenue function If it takes 4 cups of milk, 7 cups of sugar, 1 egg, 3 cups flour & 4 cups cream to make Cake 1; 3 cups milk, 4 cups sugar, 2 egg, 4 cups flour & no cream to make Cake 2; 1 cups milk, 5 cups sugar, 3 eggs, 2 cups flour & 1 cup cream to make Cake 3; 5 cups milk, no sugar, 4 eggs, 4 cups flour & 5 cups cream for Cake 4; & lastly 4 cups milk, 8 cups sugar, 5 eggs, 6 cups flour & 3 cups cream to make Cake 5; Which types of cakes to be baked such that we get maximum Revenue? Keep in mind that the store has availability of maximum 280 cups milk, 300 cups sugar, 80 eggs, 250 cups flour & 190 cups cream at their disposal. b. Formulate the constraints of the scenario. c. Solve the system if linear inequalities using Excel Solver.
Answers
A. In equation form: Revenue = 9x1 + 12x2 + 4x3 + 5x4 + 8x5
B. Non-negativity constraint: x1, x2, x3, x4, x5 ≥ 0
How did we get these values?To solve this problem using E x c e l Solver, set up the revenue function and the constraints. Here's how you can do it:
a. Revenue Function:
Let's denote the number of cakes baked for each type as x1, x2, x3, x4, and x5 respectively.
The revenue function can be formulated as:
Revenue = (Selling Price of Cake 1 × Number of Cake 1) + (Selling Price of Cake 2 × Number of Cake 2) + (Selling Price of Cake 3 × Number of Cake 3) + (Selling Price of Cake 4 × Number of Cake 4) + (Selling Price of Cake 5 × Number of Cake 5)
In equation form:
Revenue = 9x1 + 12x2 + 4x3 + 5x4 + 8x5
b. Constraints:
The constraints for the availability of ingredients can be formulated as follows:
Milk constraint: 4x1 + 3x2 + x3 + 5x4 + 4x5 ≤ 280
Sugar constraint: 7x1 + 4x2 + 5x3 ≤ 300
Egg constraint: x1 + 2x2 + 3x3 + 4x4 + 5x5 ≤ 80
Flour constraint: 3x1 + 4x2 + 2x3 + 4x4 + 6x5 ≤ 250
Cream constraint: 4x1 + 5x3 + x4 + 3x5 ≤ 190
Non-negativity constraint: x1, x2, x3, x4, x5 ≥ 0
c. Solve the system of linear inequalities using E x c e l Solver:
To solve the system of linear inequalities using E x c e l Solver, follow these steps:
1. Open M i c r o s o f t E x c e l and enter the following data in a new sheet:
| | A | B |
|-----|-----------|-----------------|
| 1 | Cakes | Selling Price |
| 2 | Cake 1 | $9 |
| 3 | Cake 2 | $12 |
| 4 | Cake 3 | $4 |
| 5 | Cake 4 | $5 |
| 6 | Cake 5 | $8 |
| | | |
| | | Formula |
| 9 | Milk | 280 |
| 10 | Sugar | 300 |
| 11 | Eggs | 80 |
| 12 | Flour | 250 |
| 13 | Cream | 190 |
2. In cell B16, enter the formula for the revenue:
=B2×B7 + B3×B8 + B4×B9 + B5×B10 + B6×B11
3. In cell B18, enter the formula for the milk constraint:
=4×B2 + 3×B3 + B4 + 5×B5 + 4×B6
4. In cell B19, enter the formula for the sugar constraint:
=7×B2 + 4×B3 + 5×B4
5. In cell B20, enter the formula for the egg constraint:
=B2 + 2×B3 + 3×B4 + 4×B5 + 5×B6
6. In cell B21, enter the formula for the flour constraint:
=3×B2 + 4×B3 + 2×B4 + 4×B5 + 6×B6
7. In cell B22, enter the formula for the cream constraint:
=4×B2 + 5×B4 + B5 + 3×B6
8. In cell B24, enter the formula for the non-negativity constraint for Cake 1:
=B2
9. Repeat step 8 for the remaining cakes, entering the formulas in cells B25, B26, B27, and B28:
=B3
=B4
=B5
=B6
10. Now, select cells B16 to B28 and click on the "Solver" button in the "Data" tab.
11. In the Solver Parameters window, set the objective to maximize the cell B16 (Revenue).
12. Set the By Changing Variable Cells to B24:B28 (the number of cakes baked).
13. Click on the "Add" button in the "Subject to the Constraints" section.
14. In the Constraint window, select the range B18:B22 for the constraint cells.
15. In the Solver Parameters window, click on the "Add" button again and select the range B24:B28 for the non-negativity constraints.
16. Set the Solver options as desired, and click on the "Solve" button.
E x c e l Solver will calculate the optimal values for the number of cakes to be baked for each type that maximize the revenue, while satisfying the given constraints on ingredient availability. The solution will be displayed in cells B24:B28, indicating the number of cakes to be baked for each type.
learn more about excel solver: https://brainly.com/question/31404959
#SPJ1
Peggy designed a pond for her backyard. She'll surround
a square patio area with a round pond. Her design and
the scale she'll use to build the design are both shown
below.
It will cost $6 per square foot to dig out the pond portion
of the yard and $1.75 per square foot to build the patio
area.
Approximately how much will she spend constructing the
pond and patio in her backyard?
Scale
1 cm = 5 ft.
A $551.80
B $1,459
C
$2.575
2 cm
2 cm
Patio
4 cm
Pond
***||| theres another answer which is D. 7,111” but it got cutt off lol|||***
Answers
Answer:Peggy will spend approximately $363.52 constructing the pond and patio in her backyard. The correct answer is not provided among the options given (A, B, C).
Step-by-step explanation:
To calculate the cost of constructing the pond and patio in Peggy's backyard, we need to determine the areas of the pond and patio and then multiply them by their respective costs per square foot.
From the given scale, we can convert the dimensions of the pond and patio from centimeters to feet. According to the scale, 1 cm represents 5 ft.
Patio dimensions:
Width: 2 cm (2 cm * 5 ft/cm = 10 ft)
Length: 2 cm (2 cm * 5 ft/cm = 10 ft)
Area of patio = Width * Length = 10 ft * 10 ft = 100 ft²
Pond dimensions:
Width: 4 cm (4 cm * 5 ft/cm = 20 ft)
Length: 4 cm (4 cm * 5 ft/cm = 20 ft)
Area of pond = π * (Width/2)² = π * (20 ft/2)² = π * 10 ft² ≈ 31.42 ft²
Cost calculation:
Cost of pond = Area of pond * Cost per square foot = 31.42 ft² * $6/ft² = $188.52
Cost of patio = Area of patio * Cost per square foot = 100 ft² * $1.75/ft² = $175.00
Total cost = Cost of pond + Cost of patio = $188.52 + $175.00 = $363.52
Heeeelp please, Can be zero or not?
with all steps and explanay.
Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
[tex]3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)[/tex]
Step-by-step explanation:
First, compute the indefinite integral:
[tex]\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x[/tex]
To evaluate the indefinite integral, use the method of substitution.
[tex]\textsf{Let} \;\;u = 4 + 3 \sin x[/tex]
Find du/dx and rewrite it so that dx is on its own:
[tex]\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u[/tex]
Rewrite the original integral in terms of u and du, and evaluate:
[tex]\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}[/tex]
Substitute back u = 4 + 3 sin x:
[tex]= \dfrac{2}{3}\sqrt{4+3\sin x}+C[/tex]
Therefore:
[tex]\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C[/tex]
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
[tex]\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}[/tex]
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
[tex]\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}[/tex]
Integrate the function between -π/2 and π/2:
[tex]\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}[/tex]
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
[tex]\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}[/tex]
To evaluate the definite integral, sum A₁, A₂ and A₃:
[tex]\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}[/tex]
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
[tex]\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}[/tex]
Therefore, the given expression cannot be zero.
A Web music store offers two versions of a popular song. The size of the standard version is 2.4 megabytes (MB). The size of the high-quality version is 4.2 MB.
Yesterday, there were 1380 downloads of the song, for a total download size of 4716 MB. How many downloads of the standard version were there?
Answers
There were 600 downloads of the standard version.
How many downloads were there?An equation means the formula that expresses the equality of two expressions by connecting them with the equals sign.
Let x represents the number of downloads of the standard version.
Given:
Size of the standard version = 2.4 MB
Size of the high-quality version = 4.2 MB
Total download size = 4716 MB
Total downloads = 1380
We will set up the following equation:
2.4x + 4.2(1380 - x) = 4716
2.4x + 5796 - 4.2x = 4716
-1.8x + 5796 = 4716
-1.8x = 4716 - 5796
-1.8x = -1080
x = 600
Read more about equation
brainly.com/question/29174899
#SPJ1
The line given by
−11x=4y+4 is dilated by a scale factor centered at the origin. The image of the line after dilation is given by
−11x−4y=16. What is the scale factor of the dilation?
Answers
The scale factor of the dilation is 4.
We are given that;
The equation of line −11x=4y+4
Now,
The center of dilation is the origin (0, 0). The line given by −11x = 4y + 4 can be rewritten as y = −11/4 x − 1. This means that it passes through the points (0, −1) and (−4, 0). The image of the line after dilation is given by −11x − 4y = 16, which can be rewritten as y = −11/4 x − 4. This means that it passes through the points (0, −4) and (−16, 0).
To find the scale factor, we can use any pair of corresponding points. For example, let’s use (0, −1) and (0, −4). The distance from the center of dilation to (0, −1) is 1 unit. The distance from the center of dilation to (0, −4) is 4 units. Therefore, the scale factor is 4/1 = 4.
Therefore, by dilation the answer will be 4
Learn more about dilation here:
https://brainly.com/question/27212783
#SPJ1
Simplify the following expression. 3 11 5 ÷ 3 − 9 5 A. 12 B. 1 81 C. 81 D.
Answers
Answer:
A
Step-by-step explanation:
To simplify the expression 3 11 5 ÷ 3 − 9 5, let's break it down step by step:
First, let's simplify the division 3 11 5 ÷ 3:
3 11 5 ÷ 3 = (3 × 115) ÷ 3 = 345 ÷ 3 = 115.
Next, let's subtract 9 5 from the result we obtained:
115 - 9 5 = 115 - (9 × 5) = 115 - 45 = 70.
Therefore, the simplified expression is 70.
The correct answer is A. 70.
Harriett designed an artistic table top for her dining room
table. Her sketch is shown below at a scale of 1 cm 6
in.
How much area will her dining room table top fill when it is
built?
5 cm
3 cm
A
B
C
D
3 cm
14 cm
9 cm
432 sq. in.
648 sq. in.
864 sq. in.
4 cm
972 sq. in.
5 cm
-
3 cm
there is also
C. 864 sq in
and
D 972 sq in
but it doesnt show
Answers
The area of the dining room table top is: 864 sq. in
How to solve scale factor problems?The formula for the area of a triangle is:
Area = ¹/₂ * base * height
Formula for the area of a rectangle is:
Area = Length * Width
Area of trapezium = ¹/₂(sum of parallel sides) * height
Thus, if 1cm = 6 inches
Then: 9cm = 54 inches
3 cm = 18 inches
4 cm = 24 inches
Thus:
Area of trapezium = ¹/₂(54 + 18) * 24
= 864 sq. in
Read more about Scale Factor at: https://brainly.com/question/25722260
#SPJ1
Please help me to do this i really need it.
First correct Answer gets Brainliest.
Answers
Answer:
Step-by-step explanation:
-3≤ x = graph 6
-3 > x = graph 3
x≥ 3 = graph 2
x ≤ 3 = graph 4
3 > x = graph 1
x > 3 = graph 5
the closed circles means greater/less than or equal to
the open circle means greater/less than
the direction of the arrow tells you if the number is greater than x or less than x
answer right all 3 and all the points go to you
Answers
The length of the arc can be obtained as follow:
Radius (r) = 7 ftAngle (θ) = 210 °Length of arc =?Length of arc = 2πr × (θ / 360)
Length of arc = (2 × π × 7) × (210 / 360)
Length of arc = 49π / 6 ft (option D)
How do i determine the area of the sector?
i. The area of the sector can be obtained as shown below:
Radius (r) = 19 inAngle (θ) = 135 °Area of sector =?Area of sector = πr² × (θ / 360)
Area of sector = (π × 19²) × (135 / 360)
Area of sector = 1083π / 8 in² (option D)
ii. The area of the sector can be obtained as shown below:
Radius (r) = 10 mAngle (θ) = 165 °Area of sector =?Area of sector = πr² × (θ / 360)
Area of sector = (π × 10²) × (165 / 360)
Area of sector = 275π / 6 m² (option B)
Learn more about length of arc:
https://brainly.com/question/31705128
#SPJ1
Susan bought a 1 kilogram bag of grapes. On the way home, she ate 125 grams of the grapes. How many grams of grapes does Susan have left? use math language and symbols to explain how you used the correct measurement units to solve the problem.
Answers
Susan has 875 grams of grapes left.
1. Susan bought a 1 kilogram bag of grapes, which is equivalent to 1000 grams (since there are 1000 grams in a kilogram).
2. Susan ate 125 grams of the grapes on her way home.
3. To find out how many grams of grapes Susan has left, we need to subtract the amount she ate from the initial weight of the bag. Therefore, we subtract 125 grams from 1000 grams.
1000 grams - 125 grams = 875 grams
4. Thus, Susan has 875 grams of grapes left.
measurement units:
In this problem, we used grams as the measurement unit. Grams are commonly used to measure the weight of small objects like grapes. Since the problem stated that Susan bought a 1 kilogram bag of grapes, it was necessary to convert the kilogram measurement to grams.
This conversion was done by multiplying the kilogram value by 1000 (1 kilogram = 1000 grams). By using the correct measurement units, we were able to accurately calculate the amount of grapes Susan had left after eating a portion.
For more such questions on grams, click on:
https://brainly.com/question/29255021
#SPJ8
A cube is sliced through the center vertically,
perpendicular to the base. The cross section that results
would be which shape? Select two that apply.
base
A
B
с
rectangle
square
trapezoid
D triangle
Answers
The cross-section that results from slicing a cube through the center vertically, perpendicular to the base, is both a rectangle and a square.
When a cube is sliced through the center vertically, perpendicular to the base, the resulting cross-section will be a rectangle and a square.
Let's consider the properties of a cube. A cube is a three-dimensional solid with six square faces. Each face of the cube is congruent and perpendicular to the adjacent faces. The edges of the cube are all equal in length, and the angles between the faces are all right angles (90 degrees).
When we slice the cube vertically through the center perpendicular to the base, we cut through the cube in such a way that the cross-section obtained is a plane figure. This cross-section will have the same shape as the face of the cube that was cut.
In this case, since the cube has square faces, the cross-section will also have the same shape. Therefore, a square is one of the shapes that apply to the resulting cross-section.
Additionally, since the slice is made through the centre of the cube, the resulting cross-section will pass through the midpoints of two opposite sides of the square face. As a result, the cross-section will have equal side lengths and parallel sides, making it a rectangle.
Final answer:
Therefore, the cross-section that results from slicing a cube through the center vertically, perpendicular to the base, is both a rectangle and a square. These shapes capture the properties of the cube's face and the nature of the cut.
For more questions on cube
https://brainly.com/question/28776132
#SPJ8
A segment with endpoints A (3, 4) and C (5, 11) is partitioned by a point B such that AB and BC form a 2:3 ratio. Find B.
Answers
The point B that partitions the segment AC into a 2:3 ratio is B (4.6, 9.6). To find the point B that partitions the segment AC into a 2:3 ratio, we can use the concept of section formulas or the concept of ratios of the coordinates.
Let's assume the coordinates of point B are (x, y). We can calculate the coordinates of point B using the following steps:
Step 1: Calculate the differences in the x and y coordinates between points A and C:
Δx = x-coordinate of C - x-coordinate of A = 5 - 3 = 2
Δy = y-coordinate of C - y-coordinate of A = 11 - 4 = 7
Step 2: Divide the differences by the sum of the ratios (2 + 3 = 5) to get the ratios of the segments AB and BC:
Ratio_AB = (2/5)[tex]\times[/tex] Δx = (2/5) [tex]\times[/tex]2 = 4/5
Ratio_BC = (3/5) [tex]\times[/tex] Δx = (3/5) [tex]\times[/tex] 2 = 6/5
Step 3: Apply the ratios to the coordinates of point A to find the coordinates of point B:
x-coordinate of B = x-coordinate of A + Ratio_AB [tex]\times[/tex] Δx = 3 + (4/5)[tex]\times[/tex]2 = 3 + 8/5 = 23/5
y-coordinate of B = y-coordinate of A + Ratio_AB [tex]\times[/tex]Δy = 4 + (4/5) [tex]\times[/tex] 7 = 4 + 28/5 = 48/5
Therefore, the coordinates of point B are (23/5, 48/5).
In decimal form, the coordinates of point B are approximately (4.6, 9.6).
For more such questions on ratio
https://brainly.com/question/2328454
#SPJ8
find the volume of this cylinder use 3 pi . 7cm 2cm
Answers
The volume of the cylinder is 98π cubic centimeters.
To find the volume of a cylinder, we use the formula:
Volume = π × [tex]r^2[/tex] × h
Given:
Radius (r) = 7 cm
Height (h) = 2 cm
Substituting the values into the formula, we have:
Volume = π × (7 [tex]cm)^2[/tex] × 2 cm
Calculating the values inside the parentheses:
Volume = π × 49 [tex]cm^2[/tex] × 2 cm
Multiplying the values:
Volume = 98π [tex]cm^3[/tex]
Therefore, the volume of the cylinder is 98π cubic centimeters.
for such more question on cylinder
https://brainly.com/question/6204273
#SPJ8
cos (α-β)/sinαcosβ = complete the identity
Answers
Answer:
consider the following data set 10 14 12 16 10 13 14 12 11 which of the relative frequency for the data value of 14
Step-by-step explanation:
1:46 AM Thu May 25
Band
AA
Savvas
Easybridge
Savvas Realize
7-3 MathXL for School: Practice & Problem Solving
Savvas Gede
Piey Blocket
empathy me...
The experimental probability of choosing the name Ted is
(Type an integer or a simplified fraction.)
EasyBridge
+
29 14% 1
Savvas Realiz-
Due 05/31/23 11:59pm
7.3.PS-12
Question Help
Challenge Nine different names were put into a hat. A name is chosen 119 times and the name Ted is
chosen 19 times. What is the experimental probability of the name Ted being chosen? What is the
theoretical probability of the name Ted being chosen? Use pencil and paper. Explain how each probability
would change if the number of names in the hat were different.
Answers
Experimental probability depends on Ted's frequency in the new set of names. The total number of names chosen also affects it. Theoretical probability is influenced by the total number of possible outcomes based on the number of names in the hat. If the number of names increases, the chance of choosing Ted decreases.
To find the experimental probability of choosing the name Ted, we divide the number of times Ted was chosen by the total number of names chosen.
Experimental probability = Number of times Ted was chosen / Total number of names chosen
Given that Ted was chosen 19 times out of 119 total selections, we can calculate the experimental probability:
Experimental probability = 19 / 119
Simplifying, we find that the experimental probability of choosing the name Ted is approximately 0.1597 or about 15.97% (rounded to the nearest hundredth).
To find the theoretical probability of choosing the name Ted, we divide the number of favorable outcomes (choosing Ted) by the total number of possible outcomes.
Theoretical probability = Number of favorable outcomes / Total number of possible outcomes
In this case, there are 9 different names in the hat, and Ted is one of them. Therefore, the theoretical probability of choosing Ted is:
Theoretical probability = 1 / 9
Simplifying, the theoretical probability of choosing the name Ted is approximately 0.1111 or about 11.11% (rounded to the nearest hundredth).
If the number of names in the hat were different, both the experimental and theoretical probabilities would change.
For the experimental probability, the number of times Ted is chosen would change based on the frequency of Ted in the new set of names. The total number of names chosen would also change.
For the theoretical probability, the total number of possible outcomes would change based on the number of names in the hat. If there were more names, the probability of choosing Ted would decrease. Conversely, if there were fewer names, the probability of choosing Ted would increase.
For more such questions on probability
https://brainly.com/question/7965468
#SPJ8