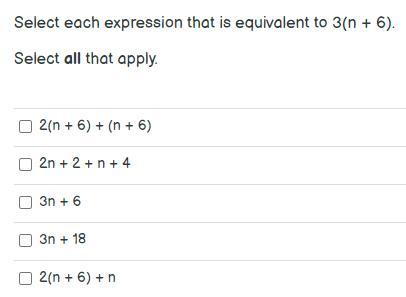Answers
Answer:
3(n + 6) = 2(n + 6) + (n + 6)
3(n + 6) = 3n + 18
Related Questions
HELP!! 10 POINTS
uhm yeah thats all I've got to say
Answers
The correct statement regarding the middle 50% of the data-set is given as follows:
C. The box, from 41 to 56.
What does a box-and-whisker plot shows?A box and whisker plots shows these five features from a data-set, listed as follows:
The minimum non-outlier value.The 25th percentile, which is the median of the bottom 50%.The median, which splits the entire data-set into two halfs, the bottom 50% and the upper 50%.The 75th percentile, which is the median of the upper 50%.The maximum non-outlier value.The box, from the 25th percentile of 41 to the 75th percentile of 56, shows the middle 50% of the data-set.
More can be learned about box plots at https://brainly.com/question/12343132
#SPJ1
Charlie made the following table to record the height of each person in his family.
If Cheyenne and Hannah lay end to end, how far will they reach?
A. 9
B. 9, 1/2
C. 10
D. 8
Answers
If you watch from ground level, a child riding on a merry-go-round will seem to be undergoing simple harmonic motion from side to side. Assume the merry-go-round is 10.6 feet across and the child completes 8 rotations in 120 seconds. Write a sine function that describes d, the child's apparent distance from the center of the merry-go-round, as a function of time t.
Answers
The sine function that describes the child's apparent distance from the center of the merry-go-round is d(t) = 5.3 sin(2π/15 * t)
How to write a sine function that describes the child's apparent distance?To write a sine function that describes the child's apparent distance from the center of the merry-go-round as a function of time t, we can start by finding the amplitude, period, and phase shift of the motion.
Amplitude:
The amplitude of the motion is half the diameter of the merry-go-round, which is 10.6/2 = 5.3 feet. This is because the child moves back and forth across the diameter of the merry-go-round.
Period:
The period of the motion is the time it takes for the child to complete one full cycle of back-and-forth motion, which is equal to the time it takes for the merry-go-round to complete one full rotation.
From the given information, the child completes 8 rotations in 120 seconds, so the period is T = 120/8 = 15 seconds.
Phase shift:
The phase shift of the motion is the amount of time by which the sine function is shifted horizontally (to the right or left).
In this case, the child starts at one end of the diameter and moves to the other end, so the sine function starts at its maximum value when t = 0. Thus, the phase shift is 0.
With these values, we can write the sine function that describes the child's apparent distance from the center of the merry-go-round as:
d(t) = 5.3 sin(2π/15 * t)
where d is the child's distance from the center of the merry-go-round in feet, and t is the time in seconds. The factor 2π/15 is the angular frequency of the motion, which is equal to 2π/T.
Learn more about sine function on:
https://brainly.com/question/30243373
#SPJ1
If anyone is reading this, rn i would be so flipping happy if u got this for me ive been waiting for so long and got nothing please answer correctly please
Answers
Answer: The answer is A.
Step-by-step explanation: Because I am smart don't underestimate me.
Answer:
C
Step-by-step explanation: (look at attachment)
3x + 4 = -2x -2
By looking at the y-intercepts, you automatically know the answer is C.
The y-intercept of the pink line is 4 because of 3x + 4.
The y-intercept of the blue line is -2, because of -2x - 2.
Using the graph, determine the equation of the axis of symmetry.
Answers
Step-by-step explanation:
x = -4 ( the value of the x-coordinate of the vertex is the axis of symmetry for normal up or down opening parabolas)
justin developed the below hypothesis. h1: younger adults (18-28 years old) spend more time on social media than the middle-aged (29-65 years old) group and older adults (older than 65 years old). what statistical test should he use to test his hypothesis?
Answers
To verify if older adults and middles ages people spend less time on social media, Justin can use the Analysis of variance (ANOVA) test.
ANOVA is used to compare means across two or more groups. Justin can use this test on the different category of younger adults, middle-aged and older adult. This test is done when there is statistically significant difference between the group of samples.
Justin can utilize post-hoc tests (such as Tukey's HSD and Bonferroni) to identify whether particular groups are statistically different from one another if an ANOVA shows a significant difference.
To know more about ANOVA test, visit,
https://brainly.com/question/30127764
#SPJ4
you place in a dark bag 24 marbles. 12 marbles are red, 5 marbles are blue and 7 marbles are yellow. you select 2 random marbles (one after the other without putting the first back in). what is the probability that the marbles have the same color?
Answers
The probability of selecting two marbles with the same color is approximately 0.27 or 27%.
To work out the likelihood that the two marbles drawn have similar variety, we can utilize the accompanying advances:
In the first place, we compute the likelihood of drawing a red marble on the principal pick: 12/24 = 1/2.
On the off chance that the main marble drawn is red, there will be 11 red marbles left clinched, out of a sum of 23 marbles. So the likelihood of drawing one more red marble on the subsequent pick is 11/23.
Likewise, in the event that the principal marble drawn is blue, there will be 4 blue marbles left clinched, out of a sum of 23 marbles. So the likelihood of drawing one more blue marble on the subsequent pick is 4/23.
Furthermore, on the off chance that the main marble drawn is yellow, there will be 6 yellow marbles left taken care of, out of a sum of 23 marbles. So the likelihood of drawing one more yellow marble on the subsequent pick is 6/23.
To get the complete likelihood of drawing two marbles of similar variety, we want to add the probabilities of every one of these cases:
(1/2) x (11/23) + (5/24) x (4/23) + (7/24) x (6/23) = 55/138 or roughly 0.398 or 39.8%.
In this way, the likelihood of drawing two marbles of a similar variety is roughly 39.8%.
To learn more about numerical on probability, refer:
https://brainly.com/question/30736519
#SPJ4
When x is 2, what is the value of the expression 124+3(8−x)12
12
4
+
3
(
8
−
x
)
12
?
Answers
When x is 2, the value of the expression is 9.
Describe Algebraic Expression?An algebraic expression is a mathematical phrase that contains one or more variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. It can also contain exponents, roots, and trigonometric functions.
Algebraic expressions are used to represent mathematical relationships and solve problems in a wide range of fields, including physics, engineering, finance, and statistics. They can be used to model real-world phenomena and to make predictions based on data.
Algebraic expressions can be simplified by combining like terms and using mathematical rules and properties. They can also be evaluated by substituting values for the variables and simplifying the expression. Solving equations involving algebraic expressions often involves manipulating the expression to isolate a variable and find its value.
When x is 2, the value of the expression 12/4+3(8−x)-12 can be found by substituting 2 for x and simplifying the expression:
12/4 + 3(8 - 2) - 12
= 3 + 3(6) - 12
= 3 + 18 - 12
= 9
Therefore, when x is 2, the value of the expression is 9.
To know more about expression visit:
https://brainly.com/question/15813344
#SPJ1
The complete question is :
When x is 2, what is the value of the expression 12/4+3(8−x)-12?
21st term: 3,8,13,18 What is the indicated term
Answers
The 21st term of the sequence 3, 8, 13, 18, .. is 103
To find the indicated term in the sequence, we first need to identify the pattern followed by the sequence. It appears that each term is obtained by adding 5 to the previous term. So, we can write the general formula for the nth term of the arithmetic sequence as
a(n) = a(1) + (n-1)d
where a(1) is the first term of the sequence, d is the common difference, and n is the term number.
In this case, we have:
a(1) = 3 (the first term)
d = 5 (the common difference)
To find the 21st term, we substitute n = 21 in the formula:
a(21) = a(1) + (21-1)d
a(21) = 3 + 20(5)
a(21) = 103
Learn more about arithmetic sequence here
brainly.com/question/16671654
#SPJ4
A rock of radioactive material has 500 atoms in it. The number of atoms decreases at a rate of 11% a day. Write an exponential function that models this situation. f(x) type your answer... (1 choose your answer... choose your answer... ✓)^x
Answers
Answer:
[tex]f(x) = 500( {.89}^{x} )[/tex]
If f(x) = 5x - 6, which of these is the inverse of f(x)?
A. f^-¹(x) = x/5 +6
B. f^-¹(x) = x/5 -6
C. f^-¹(x) = x+6/5
D. F^-¹(x) = x-6/5
Answers
To find the inverse of a function, we need to swap the positions of x and y and then solve for y. In other words, we replace f(x) with y and then solve for x.
So, let's start by swapping x and y in the function f(x) = 5x - 6:x = 5y - 6
Next, we'll solve this equation for y:
x + 6 = 5y
y = (x + 6)/5
Therefore, the inverse of f(x) is f^-1(x) = (x + 6)/5, which is option C.Find the measures of angle a and B. Round to the
nearest degree.
Answers
The measure of angle A and B is 29° and 61° respectively
What is trigonometric ratio?Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle.
sin(tetha) = opp/hyp
tan(tetha) = opp/adj
cos(tetha) = adj/hyp
The opposite is 6 and the adjascent = 11
Therefore tan (tetha) = 11/6 = 1.833
tetha = tan^-1( 1.833)
= 61°( nearest degree)
The sum of angle in a triangle is 180°
therefore,
angle A = 180-( 61+90)
= 180-151
= 29°
therefore the measure of angle A and B is 29° and 61° respectively.
learn more about trigonometric ratio from
https://brainly.com/question/24349828
#SPJ1
in a certain health center there are 3 doctors, 8 nurses and 2 physicians. in how many ways one can form a group of 5 members consisting of 1 doctor, 3 nurse and 1 physician.
Answers
Number of ways to select 1 doctor from 3 = 3C1 = 3
Number of ways to select 3 nurses from 8 = 8C3 = (8*7*6)/(3*2*1) = 56
Number of ways to select 1 physician from 2 = 2C1 = 2
Total number of ways to form the group = number of ways to select 1 doctor * number of ways to select 3 nurses * number of ways to select 1 physician
= 3 * 56 * 2
= 336
Therefore, there are 336 ways to form a group of 5 members consisting of 1 doctor, 3 nurses, and 1 physician from a health center that has 3 doctors, 8 nurses, and 2 physicians.
find the smallest which 108 must be multiplied to get a perfect square
Answers
Answer:
The answer is 3
Step-by-step explanation:
x×108=y
x×2²×3³=y
3×108=324
Quadrilateral ABCD has vertices A = (2, 5), B = (2, 2), C = (4, 3) and D = (4, 6). Quadrilateral A'B'C'D' is formed when Quadrilateral ABCD is dilated by a scale factor of 2. Which statement is true? Select all that apply
Choose all that apply:
A) None of the answers apply
B) The angles of Quadrilateral ABCD and Quadrilateral A'B'C'D' are the same.
C) The side lengths of Quadrilateral ABCD and Quadrilateral A'B'C'D' are the same.
Answers
The statement which is true for the quadrilateral is B.
How to determine which statements are true for the quadrilateral?To dilate a figure by a scale factor of 2, each point of the original figure is multiplied by 2.
So the coordinates of each vertex of A'B'C'D' are twice the coordinates of the corresponding vertex of ABCD.
The coordinates of A' are (4,10), B' are (4,4), C' are (8,6), and D' are (8,12).
To determine which statements are true, we can compare the angles and side lengths of the two quadrilaterals:
A) None of the answers apply. This may be a valid answer, but we should check the other options before concluding that none of them apply.
B) The angles of Quadrilateral ABCD and Quadrilateral A'B'C'D' are the same. This is true because dilation does not change angles. The corresponding angles of the two quadrilaterals are congruent.
C) The side lengths of Quadrilateral ABCD and Quadrilateral A'B'C'D' are not the same. We can see this by calculating the length of each side of both quadrilaterals.
Therefore, the correct answer is B.
Learn more about Quadrilateral on:
https://brainly.com/question/23935806
#SPJ1
Solve Triangle
Because I Need Answer My Assignment:-)
Good Perfect Complete=Brainlist
Copy Wrong Incomplete=Report
Good Luck Answer Brainly Users:-)
Answers
Answer:
x = 4√5 ≈ 8.94 (2 d.p.)
y = 8√5 ≈ 17.89 (2 d.p.)
Step-by-step explanation:
To find the values of x and y, use the Geometric Mean Theorem (Leg Rule).
Geometric Mean Theorem (Leg Rule)The altitude drawn from the vertex of the right angle perpendicular to the hypotenuse separates the hypotenuse into two segments. The ratio of the hypotenuse to one leg is equal to the ratio of the same leg and the segment directly opposite the leg.
[tex]\boxed{\sf \dfrac{Hypotenuse}{Leg\:1}=\dfrac{Leg\:1}{Segment\;1}}\quad \sf and \quad \boxed{\sf \dfrac{Hypotenuse}{Leg\:2}=\dfrac{Leg\:2}{Segment\;2}}[/tex]
From inspection of the given right triangle RST:
Altitude = SVHypotenuse = RT = 20Leg 1 = RS = ySegment 1 = RV = 16Leg 2 = ST = xSegment 2 = VT = 4Substitute the values into the formulas:
[tex]\boxed{\dfrac{20}{y}=\dfrac{y}{16}}\quad \sf and \quad \boxed{\dfrac{20}{x}=\dfrac{x}{4}}[/tex]
Solve the equation for x:
[tex]\implies \dfrac{20}{x}=\dfrac{x}{4}[/tex]
[tex]\implies 4x \cdot \dfrac{20}{x}=4x \cdot \dfrac{x}{4}[/tex]
[tex]\implies 80=x^2[/tex]
[tex]\implies \sqrt{x^2}=\sqrt{80}[/tex]
[tex]\implies x=\sqrt{80}[/tex]
[tex]\implies x=\sqrt{4^2\cdot 5}[/tex]
[tex]\implies x=\sqrt{4^2}\sqrt{5}[/tex]
[tex]\implies x=4\sqrt{5}[/tex]
Solve the equation for y:
[tex]\implies \dfrac{20}{y}=\dfrac{y}{16}[/tex]
[tex]\implies 16y \cdot \dfrac{20}{y}=16y \cdot \dfrac{y}{16}[/tex]
[tex]\implies 320=y^2[/tex]
[tex]\implies \sqrt{y^2}=\sqrt{320}[/tex]
[tex]\implies y=\sqrt{320}[/tex]
[tex]\implies y=\sqrt{8^2\cdot 5}[/tex]
[tex]\implies y=\sqrt{8^2}\sqrt{5}[/tex]
[tex]\implies y=8\sqrt{5}[/tex]
Number 7. I don’t understand, what’s the fraction? How do you get fraction and the + a number.
Answers
Answer:
A
Step-by-step explanation:
Equation of a line is: y = mx + b where m = slope b = y axis intercept
To find the slope between any two of the given points :
say 18, 100 and 27, 85
m = slope = (y1-y2) / (x1-x2) = (85-100) / ( 27-18) = -15/12 = -5/3
so now you have
y = - 5/3 x + b we still need to find the value of b
use any point to calculate b
say 15, 106
106 = - 5/3 (15) + b
b = ~ 131
the equation is then y = - 5/3 x + 131 closest to answer 'A'
Find the distance, d, of AB.
Answers
The distance between A and B is approximately 8.06 units.
In order to find the distance, d, of AB, we need to use the distance formula. The distance formula gives us the distance between two points in a coordinate plane. It is given as:$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ where (x1, y1) and (x2, y2) are the coordinates of the two points in question.
In this case, A and B are the two points for which we need to find the distance. Let's assume that the coordinates of A are (x1, y1) and the coordinates of B are (x2, y2).
Then the distance formula becomes:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
$$d = \sqrt{((8 + 4) - 2)^2 + ((5 - 1) - 3)^2}$$
$$d = \sqrt{(10 - 2)^2 + (4 - 3)^2}$$
$$d = \sqrt{(8)^2 + (1)^2}$$
$$d = \sqrt{64 + 1}$$
$$d \approx \sqrt{65}$$
$$d \approx 8.06$$
Therefore, the distance between A and B is approximately 8.06 units.
For more such questions on distance, click on:
https://brainly.com/question/26550516
#SPJ8
write an integral that quantifies the change in the area of the surface of a cube when its side length quadruples from s unit to 4s units.
Answers
Answer:
Step-by-step explanation:
Let A be the area of the surface of the cube.
When the side length changes from s to 4s, the new area A' can be calculated as:
A' = 6(4s)^2 = 96s^2
The change in area is then:
ΔA = A' - A = 96s^2 - 6s^2 = 90s^2
To find the integral that quantifies the change in area, we can integrate the expression for ΔA with respect to s, from s to 4s:
∫(90s^2)ds from s to 4s
= [30s^3] from s to 4s
= 30(4s)^3 - 30s^3
= 1920s^3 - 30s^3
= 1890s^3
Therefore, the integral that quantifies the change in area of the surface of a cube when its side length quadruples from s units to 4s units is:
∫(90s^2)ds from s to 4s
= 1890s^3 from s to 4s
= 1890(4s)^3 - 1890s^3
= 477,840s^3 - 1890s^3
Any help? Please. Whoever answer it first gets brainliest!
Answers
Answer:
[tex]c + 15 > 24[/tex]
[tex]c > 9[/tex]
The additional amount will be more than $9.
the anova procedure is a statistical approach for determining whether the means of . a. more than two samples are equal b. two or more populations are equal c. two samples are equal d. two or more samples are equal
Answers
The means of two or more populations being equal is determined by a statistical approach for the ANOVA procedure. Option B is correct.
The ANOVA (Analysis of Variance) procedure is a statistical method used to determine whether there is a significant difference between the means of two or more groups. To statistically test the equality of means ANOVA uses F-tests.
The repeated-measures ANOVA is a two-stage process that is described as an analysis of dependencies. This test is used to prove an assumed cause-effect relationship between variables. The conditions that must be met for the results of an ANOVA are Independence, Random Sampling, Large Sample Size, and Normality.
To learn more about the ANOVA :
https://brainly.com/question/30127764
#SPJ4
102, 107, 99, 102, 111, 95, 91
Mean
Mode
Median
Range
Answers
Answer:
mean: 101 (add all the numbers then divide by 7)
mode: 102 (the most frequent number in the set)
median: 102 (the number in the middle of the set)
range: 20 (the difference between the largest and smallest number)
Mean = 101
Mode = 102
Median = 102
Range = 20
MEAN: Add up all the numbers, then divide by how many numbers there are.
102 + 107 + 99 + 102 + 111 + 95 + 91 = 707
707 ÷ 7 = 101
MODE: Arrange all numbers in order from lowest to highest or highest to lowest and then count how many times each number appears in the set. The one that appears the most is the mode.
91,95,99,102,102,107,111
MEDIAN: Arrange the numbers from smallest to largest. If the amount of numbers is odd, the median is the middle number. If it is even, the median is the average of the two middle numbers in the list.
91,95,99,102,102,107,111
RANGE: Subtract the lowest number from the highest number
111 - 91 = 20
Three machines are used to produce nails. The table displays the total number of nails produced by the 3 machines
over different lengths of time.
Nail Production with 3 Machines
Time (minutes)
Number of Nails
(thousands)
15
16
45
48
55
593
ON
If each machine produces nails at the same rate, how many nails can 1 machine produce in 1 hour?
nails
Answers
One machine can produce 600,000 nails in one hour.
Finding the total number of nails produced by the three machines in a minute and dividing that number by three to obtain the number of nails produced by a single machine in a minute are the first two steps in the solution to this problem.
The number of nails produced by a single machine in an hour can then be calculated by multiplying that number by 60.
Now, we add up the total number of nails produced during :
(15 + 16 + 45 + 48 + 55 + 59 + 3) / 7 = 30
To find the number of nails produced by one machine in one hour, we multiply by 60: 10,000 x 60 = 600,000
To know more about multiplying, here
brainly.com/question/30875464
#SPJ4
When adding or subtracting mixed numbers with like denominators, the numerators ___ , but the denominators ______ .
A. Stay the same
B. change
Answers
Answer:
Yo, when you adding or subtracting mixed numbers with the same denominators, the numerators stay chill, they don't change, bro.
But the denominators, they also stay the same, man. It's like keeping things consistent, ya feel me? So the answer is A, dude. Numerators stay put, denominators stay put. It's all good vibes, bro! ✌️
given: weight a: 140 pounds at 17 inches aft of datum weight b: 120 pounds at 110 inches aft of datum weight c: 85 pounds at 210 inches aft of datum based on this information, the cg would be located how far aft of datum?
Answers
The center of gravity is located 96.7 inches aft of the datum.
To determine the location of the center of gravity (CG) of the system, we need to calculate the moment of each weight about the datum, and then divide the sum of the moments by the total weight of the system.
The moment of each weight is equal to its weight multiplied by its distance from the datum. In this case:
Moment of weight a = 140 pounds x 17 inches = 2,380 inch-pounds
Moment of weight b = 120 pounds x 110 inches = 13,200 inch-pounds
Moment of weight c = 85 pounds x 210 inches = 17,850 inch-pounds
The total weight of the system is:
Total weight = weight a + weight b + weight c = 140 + 120 + 85 = 345 pounds
Therefore, the location of the CG can be calculated as follows:
CG location = (Moment of weight a + Moment of weight b + Moment of weight c) / Total weight
CG location = (2,380 + 13,200 + 17,850) / 345
CG location = 33,430 / 345
CG location = 96.7 inches aft of datum
As a result, the center of gravity is 96.7 inches aft of the datum.
To know more about the Datum, here
https://brainly.com/question/15138411
#SPJ4
Maggie spent $18. 00 Of $30. 00 In her wallet which decimal represents the fraction of the $30. 00 Maggie spent
Answers
The decimal that represents the fraction of the $30.00 Maggie spent is 0.6.
Now, let's talk about decimals. Decimals are a way of expressing parts of a whole number in a fraction of 10. For example, 0.5 is the same as 1/2. In your situation, Maggie spent $18.00 out of $30.00. To figure out what decimal represents the fraction of the $30.00 Maggie spent, we need to divide the amount she spent by the total amount she had.
So, we can write this as a fraction:
$18.00 / $30.00
To turn this fraction into a decimal, we divide the numerator (top number) by the denominator (bottom number) using long division or a calculator.
$18.00 / $30.00 = 0.6
Another way to say this is that Maggie spent 60% of the money she had in her wallet.
To know more about decimal here
https://brainly.com/question/9543292
#SPJ4
The lengths of two sides of a triangle are 5.2 inches and 3.1 inches. Which lengths, in inches, could be the length of the third side?
Answers
The length of the third side between 2.1 inches and 8.3 inches (exclusive) could be a valid length for the third side of the triangle.
Triangle Inequality Theorem:In a triangle, the length of any side must be less than the sum of the lengths of the other two sides and greater than the difference between the lengths of the other two sides.
We can apply this rule to find the possible lengths of the third side of the triangle, given that the lengths of the two sides are 5.2 inches and 3.1 inches.
Here we have
The lengths of two sides of a triangle are 5.2 inches and 3.1 inches
Let's denote the length of the third side as x. Then, we have:
3.1 + 5.2 > x > 5.2 - 3.1
8.3 > x > 2.1
Therefore, the length of the third side x must be greater than 2.1 inches and less than 8.3 inches.
We can write this as an inequality:
2.1 < x < 8.3
Therefore,
The length of the third side between 2.1 inches and 8.3 inches (exclusive) could be a valid length for the third side of the triangle.
Learn more about Triangles at
https://brainly.com/question/12943336
#SPJ1
I don’t know what to write for the equation.
Answers
fraction wise, a whole is always simplified to 1, so
[tex]\cfrac{4}{4}\implies \cfrac{1000}{1000}\implies \cfrac{9999}{9999}\implies \cfrac{17}{17}\implies \text{\LARGE 1} ~~ whole[/tex]
so, we can say the whole of the players, namely all of them, expressed in fourth is well, 4/4, that's the whole lot, and we also know that 3/4 of that is 12, the guys who chose the bottle of water
[tex]\begin{array}{ccll} fraction&value\\ \cline{1-2} \frac{4}{4}&p\\[1em] \frac{3}{4}&12 \end{array}\implies \cfrac{~~ \frac{4 }{4 } ~~}{\frac{3}{4}}~~ = ~~\cfrac{p}{12}\implies \cfrac{~~ 1 ~~}{\frac{3}{4}} = \cfrac{p}{12}\implies \cfrac{4}{3}=\cfrac{p}{12} \\\\\\ (4)(12)=3p\implies \cfrac{(4)(12)}{3}=p\implies 16=p[/tex]
5 × (10 + 7) = (5 × 10) + (5 ×7)
Answers
Answer:
Same equation just using the assocaitive property
Step-by-step explanation:
For example, 8 + (2 + 3) = (8 + 2) + 3 = 13
Hope this helps! =D
how many 6 card hands are there (from a standard deck) with at least 3 kings? (enter an integer without commas)
Answers
There are 73,701 different 6-card hands (from a standard deck) with at least 3 kings.
To calculate the number of 6-card hands with at least 3 K's, the problem can be divided into:
Case 1:
Exactly 3 Kings
There are 4 ways to choose 3 kings to put in the hand, then there are 48 cards left to choose the remaining 3 cards (because we used 3 cards in a 52-card deck). Therefore, the number of 6-card hands with exactly 3 kings is:
4 * (48 choose 3) = 4 * 17,296 = 69,184
Case 2:
Exactly 4 Kings
There are 4 ways to choose 4 kings to put in the hand, then there are 48 cards left to choose the remaining 2 cards. Therefore, the number of 6-card hands with exactly 4 kings is:
4 * (48 choose 2) = 4 * 1.128 = 4.512
Case 3:
Exactly 5 kings
There are 4 ways to choose the 5 kings in the hand, then there is only one card left to choose from (because we used 5 of the 52 cards in the deck of cards). Therefore, the number of 6-card hands with exactly 5 kings is:
4*1=4
Case 4:
6 cards are king
There is only one way to choose all 6 cards as king.
Therefore, the total number of 6-card hands with at least 3 kings is:
69,184 + 4,512 + 4 + 1 = 73.701
So there are 73,701 different 6-card hands with at least 3 kings.
learn more about the deck of cards
brainly.com/question/30519560
#SPJ4