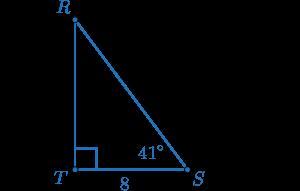
In right triangle RST, ∠T is a right angle, m∠S=41∘, and ST=8. What is the measurement of RT? Enter the correct value. If necessary, round your answer to two decimal places, like this: 42.53

Answer:

C = 2mr =

r=

m=

Step-by-step explanation:

Not sure if it's correct.

Answer:

[tex]b[/tex] ≈ [tex]12.0[/tex]

Step-by-step explanation:

Using the Pythagorean theorem: [tex]a^2+b^2=c^2[/tex] where a and b are the legs and c is the hypotenuse.

[tex]12^2+b^2=17^2\\144+b^2=289\\[/tex]

Subtract 144 from both sides

[tex]b^2=145\\[/tex]

Square root both sides

[tex]b=\sqrt{145}[/tex]

[tex]b[/tex] ≈ [tex]12.0[/tex]

Answer:

Step-by-step explanation:

[tex]12^{2} + b^{2} = 17^{2} \\144 + b^{2} = 289\\b^{2} =289-144\\b^{2} =145\\b=\sqrt{145} \\b = 12.04\\b = 12[/tex]

Hope it helps tell me if its right

Answer: 65 grams

Step-by-step explanation:

If 130 grams of a gold alloy (a mixture of gold and one or more other metals) containing 85% pure gold, you should first calculate the amount of gold that makes up this percentage.

That is, 85% of 130 grams.

85/100 × 130 = 110.5

Then, let X be what will be added to the above value to make 90%. So,

(110.5 + X) / ( 130 + X ) × 100 = 90

Divide both sides by 100

(110.5 + X) / ( 130 + X ) = 90/100

(110.5 + X) / ( 130 + X ) = 0.9

Cross multiply and open the bracket

110.5 + X = 117 + 0.9X

Collect the like terms

X - 0.9X = 117 - 110.5

0.1X = 6.5

Divide both sides by 0.1

X = 6.5/0.1

X = 65 grams

Therefore, the amount of pure gold that should be added is 65 grams

Answer:

The real part is -1

Step-by-step explanation:

The real axis is the horizontal axis

The value on the horizontal axis is -1

Answer:

B

Step-by-step explanation:

To solve this, we can make all of the numbers decimals.

π=3.14159265 and so on

Root 10 is about 3.16227766

22/7 is about 3.14285714

3.14 is already a decimal.

Now, our numbers are far easier to compare.

Let's put the numbers in increasing order.

3.14, 3.14159265, 3.14285714, 3.16227766

Substitute the original numbers in.

3.14, π, 22/7, Root 10

Therefore, option B is correct.

Answer:

Step-by-step explanation:

So if y=308x then we have to use the substitution method.

y=308x

y=122x+2338

so y=308x=122x+2338

308x-122x=186x

186x=2338

do the division and thats your answer. which is what y equals

Answer:

[tex]x[/tex] = - [tex]\frac{2y}{3}[/tex] + 2

Step-by-step explanation:

Solve for [tex]x[/tex] by simplifying both sides of the equation , isolating the variable.

Hope this helped you, Also please let me know if anything is unclear or wrong!

Answer:

Step-by-step explanation:

Answer:

I'm guessing you would like to know what -4 - 6 is? It's -10.

Step-by-step explanation:

-4 - 6 = -10

You add -4 and 6, and you get -10. I hope this helped or you meant to phrase the question differently.

Answer:

The difference between -4 and 6 is 10

Step-by-step explanation:

Hope this helps :)

Answer: The answer is the second one/b.

Answer:

D. 22/1=x/3

Step-by-step explanation:

Well what you multiply by the top you must do the bottom and opposite way also goes, sometimes so to get three as shown in (x/3) you must use the 1 from (22/1) times something to equal 3. In this it would be 1*3=3 so I multiplied three to the bottom and what I do the the bottom I haft to do to the top so 22*3=x and x is equal to 66 witch makes (D. 22/1=x/3) the correct option. If you want or need to check a good way to is to use a calculator to multiply 22*3 just as a small check up.

Answer:

The recommended daily intake of sodium for a 2000 calorie diet is 2500 mg.

Step-by-step explanation:

In order to calculate the daily intake of sodium we first need to calculate the mass of sodium present in both snacks, this is given by their sum.

[tex]\text{total sodium} = 1310 + 350 = 1660 \text{ mg}[/tex]

We can now apply a rule of three for which the total sodium from the snacks is related to 66.4% in the same proportion as "x" mg, which is the value we want to know, is related to 100%. So we have:

[tex]\frac{1660}{x} \frac{mg}{mg} = \frac{66.4\%}{100\%}[/tex]

[tex]66.4*x = 1660*100\\x = \frac{166000}{66.4} = 2500 \text{ mg}[/tex]

The recommended daily intake of sodium for a 2000 calorie diet is 2500 mg.

Answer:

2,500 mg

1,310 + 350 = 1,660

1,660 is 66.4% of 2,500

Answer:

See Explanation Below

Step-by-step explanation:

Given

[tex](sin x - cos x)^2 = sec^2x - tan^2x - 2sinx.cos x.[/tex]

Required

Prove

To start with; we open the bracket on the left hand side

[tex](sin x - cos x)^2 = (sin x - cos x)(sin x - cos x)[/tex]

[tex](sin x - cos x)^2 = (sin x )(sin x - cos x)- (cos x)(sin x - cos x)[/tex]

[tex](sin x - cos x)^2 = sin^2 x -sinx cos x - sin xcos x + cos^2 x[/tex]

[tex](sin x - cos x)^2 = sin^2 x -2sinx cos x + cos^2 x[/tex]

Reorder

[tex](sin x - cos x)^2 = sin^2 x + cos^2 x - 2sinx cos x[/tex]

From trigonometry;

[tex]sin^2x + cos^2x = 1[/tex]

So;

[tex](sin x - cos x)^2 = sin^2 x + cos^2 x - 2sinx cos x[/tex]

becomes

[tex](sin x - cos x)^2 = 1 - 2sinx cos x[/tex]

Also from trigonometry;

[tex]sec^2x - tan^2x = 1[/tex]

So,  

[tex](sin x - cos x)^2 = 1 - 2sinx cos x[/tex]

becomes

[tex](sin x - cos x)^2 = sec^2x - tan^2x - 2sinx cos x[/tex]

Proved

Answer:

Step-by-step explanation:

Circumference C=2πr  r=radius [tex]\pi =3.14[/tex]

C=2(3.14)9.7

C=60.9

Answer:

(A) It's 6/5     (B) It's 7/8  

Step-by-step explanation:

Divide each term by -6 simplify.

Hope this helped you! I don't understand the last one sorry.

Answer:

14- yes

15-No

16-11.5

Step-by-step explanation:

14- yes ( attached a picture) 5/6

15-no, because Direct Variation: It is known as the relationship between two variables where the variable quantities have a constant ratio.

8y=7x-27

     y=7/8 x-27/8

16- ky=x where k is the constant variation

k=166/83=2

ky=x when x=23

y=x/k=23/2=11.5

Answer:

The average rate of change for the amount of money is A) $25 per month

Step-by-step explanation:

From the graph we can see Sarah earn $50 every two months, 50/2 = 25/1 so we can determine Sarah's average rate of change from month 0 to month 12 is $25 dollars per month. Hope this helped, let me know if you have any questions! :)

Answer and Step-by-step explanation:

Answer:

The coordinates of C are (5 , 2)

The slope of CD is 3

The coordinates of D are (6 , 5) and (4 , -1)

Step-by-step explanation:

* Now lets study the problem

- The ends points of line AB are A = 2 , 3) and B = (8 , 1)

- CD is the perpendicular bisector of AB, and C lies on AB

- That means:

# C is the mid-point of AB

# The slope of AB × the slope of CD = -1 (one of them is a multiplicative

 inverse and additive inverse of the other)

-Ex: the slope of one is a/b, then the slope of the other is -b/a

* The mid-point between two points (x1 , y1) and (x2 , y2) is:

 [(x1 + x2)/2 , (y1 + y2)/2]

∵ C is the mid-point of AB

∴ C = [(2 + 8)/2 , (3 + 1)/2] = [10/2 , 4/2] = (5 , 2)

* The coordinates of C are (5 , 2)

- The slope of a line passing through points (x1 , y1) and (x2 , y2) is:

the slope = (y2 - y1)/(x2 - x1)

∴ The slope of AB = (1 - 3)/(8 -2) = -2/6 = -1/3

∵ CD ⊥ AB

∴ The slope of CD × the slope of AB = -1

∴ The slope of CD = 3

* The slope of CD is 3

- The length of a line passing through points (x1 , y1) and (x2 , y2) is:

the length = √[(x2 - x1)² + (y2 - y1)²]

∵ The length of CD = √10

∵ Point D is (x , y)

∴ (x - 5)² + (y - 2)² = (√10)²

∴ (x - 5)² + (y - 2)² = 10 ⇒ (1)

∵ The slope of CD is (y - 2)/(x - 5) = 3 ⇒ by using cross multiply

∴ (y - 2) = 3(x - 5) ⇒ (2)

- Substitute (2) in (1)

∴ (x - 5)² + [3(x - 5)]² = 10 ⇒ simplify

* [3(x - 5)]² = (3)²(x - 5)² = 9(x - 5)²

∴ (x - 5)² + 9(x - 5)² = 10 ⇒ add the like terms

∴ 10(x - 5)² = 10 ⇒ ÷ 10 both sides

∴ (x - 5)² = 1 ⇒ take √ for both sides

∴ x - 5 = ± 1

∴ x - 5 = 1 ⇒ add 5 to both sides

∴ x = 6

* OR

∴ x - 5 = -1 ⇒ add 5 to both sides

∴ x = 4

- Substitute the values of x in (2)

∴ y - 2 = 3(6 - 5)

∴ y - 2 = 3 ⇒ add 2

∴ y = 5

* OR

∴ y - 2 = 3(4 - 5)

∴ y - 2 = -3 ⇒ add 2

∴ y = -1

* The coordinates of D are (6 , 5) and (4 , -1)

Answer:

D

Step-by-step explanation:

The figure A will be translated 6 units to the left to make it on figure B

Answer:

27 Oz of 25% alcohol

Step-by-step explanation:

--percent ---------------- quantity

Alcohol I 30 ---------------- 18 Oz

alcohol II 25 ---------------- x Oz

Mixture 27 ---------------- 18 + x Oz

30*18+25x=27(18+x)

540+25x =486+27 x

25x-27x =486+540

-2x=-54

/ -2

x = 27

27 Oz of 25% alcohol

Answer:

Step-by-step explanation:

Answer:

C. Multiply 3 by 18

Step-by-step explanation:

Susan reads:

1 page in 3 mins

So,

1 page = 3 mins

If we want the time for 18 pages, we would multiply both sides by 18

So,

18 pages = 3×18 mins

18 pages = 54 mins

Answer:

C

Step-by-step explanation:

1 page every 3 minutes

18 pages will take 3 × 18 = 54 minutes to read.

Answer:

Option C.

Step-by-step explanation:

It is given that James earns $1000 weekly base pay as a sales-person.

We know that, we have 4 weeks in a month. So, monthly salary of james is

Monthly income [tex]=\$1000\times 4=\$4,000[/tex]

It is said that he sold $20,000 worth of merchandise last month and he gets a 10% commission on everything he sells.

Commission [tex]=\$20,000\times \dfrac{10}{100}=\$2,000[/tex]

Total amount = Monthly income + Commission

          [tex]=\$4,000+\$2,000[/tex]  

          [tex]=\$6,000[/tex]  

Therefore, the correct option is C.

Answer:

40

Step-by-step explanation:

The sum equals 80 80/2=40

Answer:

3

Step-by-step explanation: If you write out all the numbers and you cross them out in order you will find that 3 is your median.

Answer:

B

Step-by-step explanation:

The question is asking for what y would be when x is 2.

So, look on the graph where x = 2.

When x = 2, y = 6.

This means after 2 hours, the cost is $6

Answer:

Rs 60

Step-by-step explanation:

[tex]5x \times (1+25\%)+5x \times (1-16\frac{2}{3}\%)=625[/tex]

[tex]5x(1+0.25)+5x(1-1/6)=625[/tex]

[tex]5x(1.25)+5x(5/6)=625[/tex]

[tex]10.416667x=625[/tex]

[tex]\frac{10.416667x}{10.416667}=\frac{625}{10.416667}[/tex]

[tex]x=59.99999...[/tex]

[tex]x=60[/tex]

Answer:

65°

Step-by-step explanation:

180°-50°:130°

130°÷2:65°

130° divide by 2 because the shape was isosceles triangle

Answer:

36 degrees.

Step-by-step explanation:

All the angles in a triangle add up to be 180 degrees. Since the ratio is 1:2:2, you can say that the angles are x, 2x, and 2x.

x + 2x + 2x = 180

5x = 180

x = 180 / 5

x = 36

Since the smallest part of the ratio is 1, the smallest angle is 36 degrees.

Hope this helps!

Answer:

x<12

Step-by-step explanation:

Divide both sides by 5

5(x+5) < 85

   5         5      

then simply

Answer:

x < 12

Step-by-step explanation:

[tex]5(x+5)<85\\\\5 * x = 5x\\\\5 * 5 = 25\\\\5x+25<85\\\\5x+25-25<85-25\\\\5x<60\\\\\frac{5x}{5}<\frac{60}{5}\\ \boxed{x<12}[/tex]

Answer: If you want to make more cookies then what is called for in this situation then you would need 6 cups of milk.

Step-by-step explanation: You have 2 cups of milk and 3 cups of flour of course. In order to make a complete batch you need 2 cups of milk and 3 cups of flour. In order to make a second batch you need the same things as you did for the first batch. Therefore two batches of cookies requires 4 cups of milk and 6 cups of flour. In this situation you want to make 3 batches of cookies. The required items are 6 cups of milk and 9 cups of flour.

Answer:

(6, 2)

Step-by-step explanation:

Step 1: Use substitution

x - 4 = 1/3x

Step 2: Isolate x

2/3x = 4

x = 6

Step 3: Plug back into original equation(s)

y = 6 - 4

y = 2

Answer:

(6,2)

Step-by-step explanation:

Let's use the substitution method.

x-4=1/3x

3x-12=x

3x=x+12

2x=12

x=6

y=6-4

y=2

Answer:

B

2(6)+4 > 16             x > 6                 2(7) + 4 > 16

12+4=16                                            14+4>16       18>16