Answers
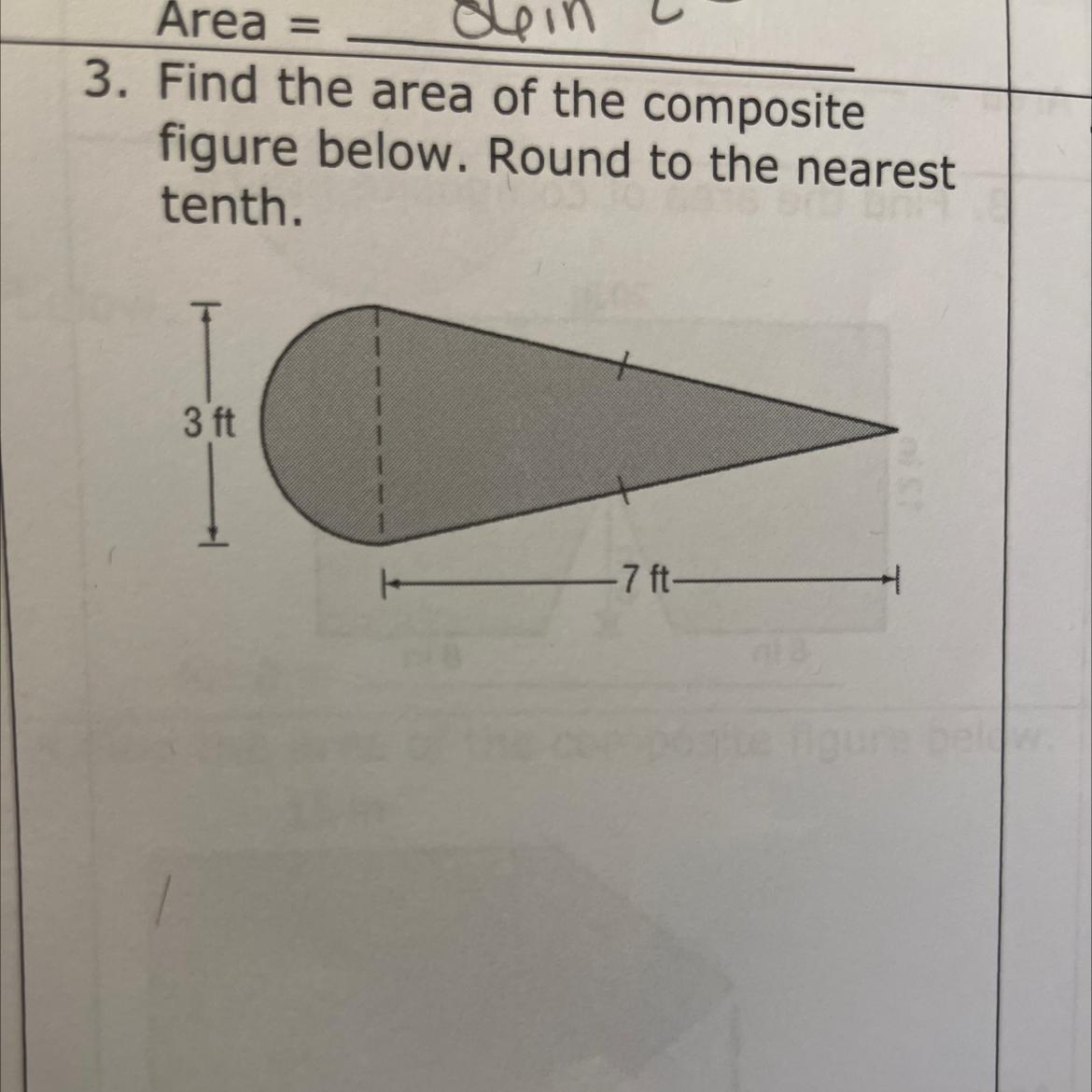
The total area of the figure with of the semicircle and triangle is 12.27 sq. ft.
What is semicircle?Half of a circle is known as a semicircle, and the diameter of the circle is equal to the length of the semicircle's straight edge. A sector of a circle is a section of a circle that is bounded by an arc, two radii, and both. A semicircle is always half of a circle and has a constant central angle of 180 degrees, but a sector can be any part of a circle and has a central angle that can vary from 0 to 360 degrees. This is the major distinction between the two.
Given, the diameter of the semicircle is 3 ft, so its radius is 1.5 ft.
Now, area of the semicircle is given as:
A = 1/2 * pi * (1.5)² = 1.77 sq ft
The area of the triangle is:
A = 1/2 * 3 ft * 7 ft = 10.5 sq ft
Adding the areas we have the total area of the figure:
1.77 sq ft + 10.5 sq ft = 12.27 sq ft
Hence, the total area of the figure is 12.27 sq. ft.
Learn more about area of semicircle here:
https://brainly.com/question/16952186
#SPJ1
Related Questions
a trapezoid has an area of 96 ft. if the base is 11 feet and the height is 8 feet, what is the length of the other base
Answers
Answer:
The formula for the area of a trapezoid is:
Area = (b1 + b2) / 2 x h
where b1 and b2 are the lengths of the two parallel bases, and h is the height.
We are given that the area of the trapezoid is 96 ft, the height is 8 ft, and one of the bases (b1) is 11 ft. We can use this information to find the length of the other base (b2).
Substituting the given values into the formula for the area of a trapezoid, we get:
96 = (11 + b2) / 2 x 8
Multiplying both sides by 2 and dividing by 8, we get:
24 = 11 + b2
Subtracting 11 from both sides, we get:
b2 = 13
Therefore, the length of the other base is 13 ft.
Evan takes 100 milligrams of medicine. The amount of medicine in his bloodstream decreases by 0.4 milligram each minute for a number of minutes, m, after that. He writes the expression 100 - 0.4m to find the amount of medicine in his bloodstream after m minutes. Which statement about his expression is true?
Answers
The statement that is true about Evan's expression is that it represents a linear function of the amount of medicine in his bloodstream, where the initial amount is 100 milligrams and the rate of change is -0.4 milligrams per minute.
What is the equivalent expression?
Equivalent expressions are expressions that perform the same function despite their appearance. If two algebraic expressions are equivalent, they have the same value when we use the same variable value.
The expression 100 - 0.4m represents the amount of medicine in Evan's bloodstream after m minutes, where the amount of medicine decreases by 0.4 milligrams each minute.
The coefficient of the variable m (-0.4) represents the rate of change of the amount of medicine in Evan's bloodstream per minute. It tells us that for every one minute that passes, the amount of medicine in his bloodstream decreases by 0.4 milligrams.
The constant term (100) represents the initial amount of medicine in Evan's bloodstream before the medicine starts to decrease.
Therefore, the statement that is true about Evan's expression is that it represents a linear function of the amount of medicine in his bloodstream, where the initial amount is 100 milligrams and the rate of change is -0.4 milligrams per minute.
To learn more about the equivalent expression visit:
https://brainly.com/question/2972832
#SPJ1
An industrial/organizational psychologist has been consulting with a company that runs weekend job-seeking workshops for the unemployed. She collected data on several issues related to these workshops and, after conducting statistical tests, obtained statistically significant findings. She needs to find a way to evaluate effect size so that she can make recommendations to the company. One of the psychologist's findings is that 18 months after the workshop, a sample of 81 job seekers who received training on using the Internet to find job listings worked more than 30 hours per week an average of 8. 7 months in the last year, with a standard deviation of 4. 1. The typical job seeker works 7. 4 months. The psychologist finds that the estimated Cohen's d is _____, the t statistic is 2. 83, and r^2 is ______. Using Cohen's d and Cohen's guidelines for interpreting the effect size with the estimated Cohen's d, there is a ______ treatment effect. Using r^2 and the extension of Cohen's guidelines for interpreting the effect size using r^2, there is a ______ treatment effect. Another one of the psychologist's findings is that a sample of 81 job seekers who received training on interview skills scored an average of 8. 1 as measured on a 9-point job search motivation scale, with a standard deviation of. 8. The typical job seeker scores 7. 4 points. She finds that the estimated Cohen's d is _____, the t statistic is 7. 78, and r^2 is _____ Using Cohen's d and Cohen's guidelines for interpreting the effect size with the estimated Cohen's d, there is a treatment effect. Using r^2 and the extension of Cohen's guidelines for interpreting the effect size with r^2, there is a ___ treatment effect
Answers
The psychologist finds that the estimated Cohen's d is 0.32, the t statistic is 2. 83, and r² is 0.073. Using r² and the extension of Cohen's guidelines for interpreting the effect size using r², there is a small treatment effect. job seeker finds that the estimated Cohen's d is 0.88, the t statistic is 7. 78, and r² is 0.479.Using r² and the extension of Cohen's guidelines for interpreting the effect size with r², there is a large treatment effect
To calculate the estimated Cohen's d, we use the formula
d = (M - M0) / SD
where M is the mean of the treatment group (job seekers who received training on using the Internet to find job listings), M0 is the mean of the control group (typical job seeker), and SD is the pooled standard deviation of the two groups. Using the given values, we have
M = 8.7 months
M0 = 7.4 months
SD = 4.1 months
So, d = (8.7 - 7.4) / 4.1 = 0.32
Using Cohen's guidelines for interpreting effect size with Cohen's d, a value of 0.2 is considered a small effect, 0.5 a medium effect, and 0.8 a large effect. Therefore, with an estimated Cohen's d of 0.32, there is a small treatment effect.
To calculate r², we use the formula
r² = t² / (t² + df)
where t is the t statistic, df is the degrees of freedom (n-2 for a two-group design), and n is the sample size. Using the given values for the Internet training group, we have
t = 2.83
n = 81
df = 79
So, r² = 2.83² / (2.83² + 79) = 0.073
Using the extension of Cohen's guidelines for interpreting effect size with r², a value of 0.01 is considered a small effect, 0.09 a medium effect, and 0.25 a large effect. Therefore, with an r² of 0.073, there is a small treatment effect.
For the job seekers who received training on interview skills, we can calculate Cohen's d and r² in a similar way
d = (M - M0) / SD = (8.1 - 7.4) / 0.8 = 0.88
t = 7.78
n = 81
df = 79
r² = 7.78² / (7.78² + 79) = 0.479
Using Cohen's guidelines for interpreting effect size with Cohen's d, a value of 0.2 is considered a small effect, 0.5 a medium effect, and 0.8 a large effect. Therefore, with an estimated Cohen's d of 0.88, there is a large treatment effect.
Using the extension of Cohen's guidelines for interpreting effect size with r², a value of 0.01 is considered a small effect, 0.09 a medium effect, and 0.25 a large effect. Therefore, with an r² of 0.479, there is a medium to large treatment effect.
To know more about estimated Cohen's d:
https://brainly.com/question/31427772
#SPJ4
Answer:.317
.091
Small to med
Med
.875
.431
Large
Large
Step-by-step explanation:
angles of triangles- does anyone know how to do this?
Answers
(1) m∠1=45°(sum of 3 angles of a triangle is always 180°)
(2) m∠1=180°-129°=51°(sum of two interior angles on the same side is equal to the exterior angle)
(3) m∠1= 152°-115°=37°
(4) m∠1=88°m∠2=42° m∠3=113°
What is an angle?An angle is a geometric figure formed by two rays that share a common endpoint, called the vertex. The measure of an angle is typically expressed in degrees or radians, and it describes the amount of rotation needed to bring one of the rays into coincidence with the other.
Define triangle?A triangle is a closed two-dimensional shape with three straight sides and three angles.
(1) m∠1=45°(sum of 3 angles of a triangle is always 180°)
(2) m∠1=180°-129°=51°(sum of two interior angles on the same side is equal to the exterior angle)
(3) m∠1= 152°-115°=37°(sum of two interior angles on the same side is equal to the exterior angle)
(4) m∠1=88°(sum of 3 angles of a triangle is always 180°),m∠2=42°(vertically opposite angle theorem), m∠3=113°(sum of 3 angles of a triangle is always 180°)
Learn more about angles here:
https://brainly.com/question/28451077
#SPJ1
Recall the equation for a circle with center (h, k) and radius r. At what point in the first quadrant does
the line with equation y = 2z+ 3 intersect the circle with radius 3 and center (0, 3)?
Answers
The point of intersection in the first quadrant is (3, 4) from the equation of circle.
Equation of circle.
We can start by substituting the equation of the line into the equation of the circle and solving for z and y.
The equation for the circle is:
(x - h)^2 + (y - k)^2 = r^2
Substituting h = 0, k = 3, and r = 3, we get:
x^2 + (y - 3)^2 = 9
Now, we substitute y = 2z + 3 into the equation:
x^2 + (2z + 3 - 3)^2 = 9
Simplifying, we get:
x^2 + 4z^2 = 9
Since we are looking for a point in the first quadrant, both x and z must be positive. We can solve for z in terms of x:
4z^2 = 9 - x^2
z^2 = (9 - x^2)/4
z = sqrt[(9 - x^2)/4]
Substituting this into the equation y = 2z + 3, we get:
y = 2sqrt[(9 - x^2)/4] + 3
To find the point of intersection in the first quadrant, we need to find a value of x that satisfies both this equation and the equation of the circle. We can substitute the equation for y into the equation for the circle:
x^2 + [2sqrt((9 - x^2)/4)]^2 = 9
Simplifying, we get:
x^2 + (9 - x^2)/2 = 9
Multiplying both sides by 2:
2x^2 + 9 - x^2 = 18
Solving for x:
x^2 = 9
x = 3
Substituting x = 3 into the equation for y, we get:
y = 2sqrt[(9 - 3^2)/4] + 3 = 4
Therefore, the point of intersection in the first quadrant is (3, 4).
Learn more about equation of circle below.
https://brainly.com/question/1506955
#SPJ1
A small can of tomato paste has a radius of 2 inches and a height of 4 inches. Suppose the larger, commercial-size can has dimensions that are related by a scale factor of 3. Which of these is true?
Answers
The correct statement about scale factor is the radius of the larger can will be 8 inches. (option c).
Let's first consider the dimensions of the small can of tomato paste. We are given that it has a radius of 2 inches and a height of 4 inches. Therefore, its volume can be calculated using the formula for the volume of a cylinder, which is V = πr²h, where V is the volume, r is the radius, and h is the height. Substituting the given values, we get:
V_small = π(2²)(4) = 16π cubic inches
Using these dimensions, we can calculate the volume of the larger can using the same formula:
V_large = π(6²)(12) = 432π cubic inches
Now, let's compare the volumes of the small and large cans. We have:
V_large = 432π cubic inches > 16π cubic inches = V_small
Therefore, we can conclude that the volume of the larger can is greater than the volume of the smaller can. But is it three times greater? Let's compare:
V_large = 432π cubic inches 3
V_small = 3(16π) cubic inches = 48π cubic inches
We see that 432π cubic inches is not equal to 48π cubic inches, so option b) is not correct.
Finally, let's consider the radius of the larger can. We found earlier that it is 6 inches, which is greater than the radius of the smaller can, but it is not 8 inches. Therefore, option c) is correct.
To know more about scale factor here
https://brainly.com/question/30215119
#SPJ4
Complete Question:
A small can of tomato paste has a radius of 2 inches and a height of 4 inches. Suppose the larger, commercial-size can has dimensions that are related by a scale factor of 3. Which of these true?
a) The radius of the larger can will be 5 inches.
b) The volume of the larger can will be 3 times the volume of the smaller can
c) The radius of the larger can will be 8 inches.
d) The volume of the larger can is 3 times the volume of smaller can
9.12 movie lovers, part ii. suppose an online media streaming company is interested in building a movie recommendation system. the website maintains data on the movies in their database (genre, length, cast, director, budget, etc.) and additionally collects data from their subscribers ( demographic information, previously watched movies, how they rated previously watched movies, etc.). the recommendation sys- tem will be deemed successful if subscribers actually watch, and rate highly, the movies recommended to them. should the company use the adjusted r2 or the p-value approach in selecting variables for their recommendation system?
Answers
The company should use the adjusted R² approach to select variables for their recommendation system, as it will better account for the influence of multiple variables and help create a more accurate model for predicting subscriber's movie ratings.
To build a successful movie recommendation system for the online media streaming company, it's important to consider the appropriate statistical approach for selecting variables.
In this case, the company should use the adjusted R² approach instead of the p-value approach.
The adjusted R² approach is more suitable for this scenario because it measures the proportion of variance in the dependent variable (subscriber's ratings) that is predictable from the independent variables (movie and subscriber data).
Adjusted R² takes into account the number of variables and adjusts for overfitting, which is important when dealing with a large dataset, like the one the streaming company has.
It helps in identifying the most influential factors and creating a model that better predicts movie ratings.
On the other hand, the p-value approach focuses on the statistical significance of individual variables, which might lead to including variables that are significant but not necessarily the best predictors for movie ratings.
This could result in a less accurate recommendation system.
For similar question on proportion.
https://brainly.com/question/11941144
#SPJ11
how do i solve this trigonometry question?
Answers
Answer:
2.07 cm
Step-by-step explanation:
Hypotenuse = 2 cm
Adjacent side = a
Formula
cos θ = Hypotenuse/Adjacent side
cos 15 = 2/a
Note
The value of cos 15 is approximately 0.965.
0.965 = 2/a
a = 2/0.965
a = 2.07 cm ( approximately )
a cylinder has a radius of 3 cm and a height of 8 cm. what is the longest segment, in centimeters, that would fit inside the cylinder?
Answers
The longest segment that would fit inside the cylinder is approximately 9.06 centimeters.
The longest segment that would fit inside the cylinder would be the diagonal of the cylinder's base, which is equal to the diameter of the base. The diameter of the base is equal to twice the radius, so it is 6 cm. Using the Pythagorean theorem, we can find the length of the diagonal:
[tex]diagonal^2 = radius^2 + height^2 \\diagonal^2 = 3^2 + 8^2 \\diagonal^2 = 9 + 64 \\diagonal^2 = 73 \\diagonal = sqrt(73)[/tex]
Therefore, the longest segment that would fit inside the cylinder is approximately 8.54 cm (rounded to the nearest hundredth).
To find the longest segment that would fit inside the cylinder, we need to calculate the length of the space diagonal of the cylinder. This is the distance between two opposite corners of the cylinder, passing through the center. We can use the Pythagorean theorem in 3D for this calculation.
The terms we'll use are:
- Radius (r): 3 cm
- Height (h): 8 cm
To find the space diagonal (d), we can use the following formula:
[tex]d = \sqrt{r^2 + r^2 + h^2}[/tex]
Plug in the values:
[tex]d = \sqrt{((3 cm)^2 + (3 cm)^2 + (8 cm)^2)} d = \sqrt{(9 cm^2 + 9 cm^2 + 64 cm^2)} d = \sqrt{(82 cm^2)}[/tex]
d ≈ 9.06 cm
Learn more about cylinder here:
https://brainly.com/question/23991640
#SPJ11
The longest segment that can fit inside the cylinder is. [tex]$\sqrt{73}$ cm[/tex].
The longest segment that can fit inside a cylinder is a diagonal that connects two opposite vertices of the cylinder.
The length of this diagonal by using the Pythagorean theorem.
Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle.
It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.
This theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, often called the Pythagorean equation:[1]
[tex]{\displaystyle a^{2}+b^{2}=c^{2}.}[/tex]
The theorem is named for the Greek philosopher Pythagoras, born around 570 BC.
The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem.
The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.
Consider a right triangle with legs equal to the radius.
[tex]$r$[/tex] and the height [tex]$h$[/tex] of the cylinder, and with the diagonal as the hypotenuse.
Then, by the Pythagorean theorem, the length of the diagonal is:
[tex]$\sqrt{r^2 + h^2} = \sqrt{3^2 + 8^2} = \sqrt{73}$[/tex]
For similar questions on cylinder
https://brainly.com/question/23935577
#SPJ11
5. Select Yes or No to indicate whether each ordered pair is a point of intersection
between the line x - y = 6 and the circle y² - 26 = -x².
Ordered Pair
(1,-5)
(1,5)
(5,-1)
Answers
To determine if each ordered pair is a point of intersection between the line x - y = 6 and the circle y² - 26 = -x², we need to substitute the values of x and y in both equations and see if they are true for both.
Select Yes or No to indicate whether each ordered pair is a point of intersectionFor the ordered pair (1, -5):
x - y = 6 becomes 1 - (-5) = 6, which is true.
y² - 26 = -x² becomes (-5)² - 26 = -(1)², which is false.
Therefore, (1, -5) is not a point of intersection.
For the ordered pair (1, 5):
x - y = 6 becomes 1 - 5 = -4, which is false.
y² - 26 = -x² becomes (5)² - 26 = -(1)², which is true.
Therefore, (1, 5) is a point of intersection.
For the ordered pair (5, -1):
x - y = 6 becomes 5 - (-1) = 6, which is true.
y² - 26 = -x² becomes (-1)² - 26 = -(5)², which is false.
Therefore, (5, -1) is not a point of intersection.
So the answer is:
(1,-5) - No
(1,5) - Yes
(5,-1) - No
to know more about equations
brainly.com/question/29657983
#SPJ1
All help is appreciated thank you.
Answers
Using the fact that the triangles are similar we can see that the value of x is 36
How to find the value of x?We can see that the triangles are similar due to the same interior angles, then ther is a scale factor k between them.
So we can write:
20*k = 48
k = 48/20 = 2.4
Then:
x = 15*2.4
x = 36
That is the value of x.
Learn more about similar triangles at:
https://brainly.com/question/14285697
#SPJ1
The answers are in the picture. I need help ASAP!
Answers
The perimeter and the area of the regular polygon are 20 inches and 27.53 square inches.
How to calculate the area and the perimeter of a regular polygon
The figure representing a regular polygon with five sides of same length, whose perimeter and area is well described by following formulas:
Perimeter
p = n · l
Area
A = (n · l · a) / 2
Where:
A - Area of the polygon, in square inches. n - Number of sides.l - Side length, in inches. a - Apothema, in inches. p - Perimeter, in inches.Where the apothema is:
a = 0.5 · l / tan (180° / n)
If we know that l = 4 in and n = 5, then the perimeter and the area of the polygon are:
Perimeter
p = 5 · (4 in)
p = 20 in
Area
a = 0.5 · (4 in) / tan (180° / 5)
a = 0.5 · (4 in) / tan 36°
a = 2.753 in
A = [5 · (4 in) · (2.753 in)] / 2
A = 27.53 in²
To learn more on area of regular polygons: https://brainly.com/question/12291395
#SPJ1
A tram moved downward 12 meters in 4 seconds at a constant rate. What was the change in the tram's elevation each second?
Answers
Therefore , the solution of the given problem of unitary method comes out to be during the 4-second period, the tram's elevation changed by 3 metres every second.
What is an unitary method?To complete the assignment, use the iii . -and-true basic technique, the real variables, and any pertinent details gathered from basic and specialised questions. In response, customers might be given another opportunity to sample expression the products. If these changes don't take place, we will miss out on important gains in our knowledge of programmes.
Here,
By dividing the overall elevation change (12 metres) by the total time required (4 seconds),
it is possible to determine the change in the tram's elevation every second. We would then have the average rate of elevation change per second.
=> Elevation change equals 12 metres
=> Total duration: 4 seconds
=> 12 meters / 4 seconds
=> 3 meters/second
As a result, during the 4-second period, the tram's elevation changed by 3 metres every second.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
Sam makes tote bags for a school fundraiser. The fixed costs for making the bags is $30. The cost of the materials for each bag is $8.50. Sam can spend less than a total of $200 on the tote bags. Write an inequality that can be used to determine b , the number of tote bags that can be made.
Answers
8.50b + 30 ≤ 200
where b is the number of tote bags that can be made, 8.50 is the cost of materials for each bag, 30 is the fixed cost, and 200 is the maximum allowable spending on the tote bags.
This is precalc trig please help
Answers
The answer to the trigonometry question in the picture attached is:
= cos θ / [sin θ * (1 - sin θ)] * (1 + sin θ)
Here is the step by step approach to solving the trigonometrySimplify 1-csc θ as follows:
1 - csc θ = (1 - csc θ)(1 + csc θ) / (1 + csc θ)
= 1 - csc^2 θ / (1 + csc θ)
= 1 - 1/sin^2 θ / (1 + 1/sin θ)
= 1 - sin^2 θ / (sin θ + 1)
= (sin θ - sin^2 θ) / (sin θ + 1)
Simplify 1+csc θ as follows:
1 + csc θ = (1 + csc θ)(1 - csc θ) / (1 - csc θ)
= 1 - csc^2 θ / (1 - csc θ)
= 1 - 1/sin^2 θ / (1 - 1/sin θ)
= 1 - sin^2 θ / (sin θ - 1)
= (sin θ + sin^2 θ) / (sin θ - 1)
Substitute the above simplifications in the expression cos θ/(1-csc θ) * 1+csc θ/(1+ csc θ) to get:
cos θ / (sin θ - sin^2 θ) * (sin θ + sin^2 θ) / (sin θ + 1)
Simplify the expression by canceling out the sin^2 θ terms:
cos θ / (sin θ - sin^2 θ) * (sin θ + sin^2 θ) / (sin θ + 1)
= cos θ / (sin θ - sin^2 θ) * (1 + sin θ) / (sin θ + 1)
Simplify further by factoring out common terms in the numerator and denominator:
cos θ / (sin θ - sin^2 θ) * (1 + sin θ) / (sin θ + 1)
= cos θ * (1 + sin θ) / [(sin θ - sin^2 θ) * (sin θ + 1)]
Finally, simplify the expression by factoring out a sin θ term from the denominator:
cos θ * (1 + sin θ) / [(sin θ - sin^2 θ) * (sin θ + 1)]
= cos θ * (1 + sin θ) / [sin θ * (1 - sin θ) * (sin θ + 1)]
= cos θ / [sin θ * (1 - sin θ)] * (1 + sin θ)
Learn more about Trigonometry here:
https://brainly.com/question/25618616
#SPJ1
Find the measure of the line segment indicated, assume that lines which appear tangent, are tangent.
Find FS
Possible answers —>
A. 17
B. 21
C. None of the other answers are correct
D. 18
E. 45
Answers
The value of x for the intersecting chords is derived to be 1.9 and the segment FS is equal to 18
What is the properties of intersecting chordsThe property of intersecting chords states that in a circle, if two chords intersect, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.
UF × FS = VF × FT
8(10x - 1) = 9 × 16
80x - 8 = 144
80x = 144 + 8 {collect like terms}
80x = 152
x = 152/80 {divide through by 80}
x = 1.9
FS = 10(1.9) - 1 = 18
Therefore, the value of x for the intersecting chords is derived to be 1.9 and the segment FS is equal to 18
Read more about intersecting chords here:https://brainly.com/question/13950364
#SPJ1
I need help with this question can you help?
Answers
Answer:
The Correct answer is sinA/3.2=sin110°/4.6
Find the measure of the missing side.
1. 8.2
2. 9.9
3. 7.4
4. 10.9
Answers
Answer:
1
Step-by-step explanation:
First of all we use the "law of sines"
to get the measure/length we need the opposing angle of it of the side, now in this case the missing side is x
and its opposing angle is missing so using common sense, the sum of angles in the triangle is 180°
180°=70°+51°+ x
x = 180°-121°
=59°
Using law of sines:
(sides are represented by small letters/capital letters are the angles)
a/sinA= b/sinB= c/sinC
We have one given side which is "9"
so,
9/sin70= x/sin59
doing the criss-cross method,
9×sin59=sin70×x
9×sin59/sin70=x
x=8.2 (answer 1)
I hope this was helpful <3
help me please please
Answers
x^4 * x^3 = x^12
Rule: multiply exponents you multiply coefficients but add the exponents.
*They multiplied the exponents
✅ = x^7
4w^5 * 5w^7 = 9w^12
Rule: multiply exponents you multiply coefficients but add the exponents,
*they added the coefficients
✅ = 20w^12
( g^2)^5
Rule: exponent of exponent you multiply the exponents,
*they added the exponents
✅ g^10
(2m^3)^4 = 2m^12
Rule: exponent of exponent with coefficient, distribute the outside exponent to the terms inside the parentheses, simplify the terms and combine them. * they only multiplied the exponents and neglected the coefficient term.
2^4 and (m^3)^4
16 and m^12
combine both terms
✅ 16m^12
y^-2 * y*5 = y^3
✅ this one is correct, add the exponents
-2 + 5 = 3 exponent, so y^3
2k^0 = 1
Rule; exponent of 0 zero makes the term value 1, * they made the whole term 1 and neglected the coefficient
✅ (2)(1) = 2
f^6 + f^1 = f^7
Rule: you cannot add unlike terms. It’s like adding apples and oranges. You cannot add f^6 and f^1, they are not the same. *they multiplied instead of added
So your answer is
✅ f^6 + f^1
ASAP I really need help doing a two column proof for this please.
Answers
The two column proof is written as follows
Statement Reason
MA = XR given (opposite sides of rectangle)
MK = AR given (opposite sides of rectangle)
arc MA = arc RK Equal chords have equal arcs
arc MK = arc AK Equal chords have equal arcs
Equal chords have equal arcsAn arc is a portion of the circumference of a circle, and a chord is a line segment that connects two points on the circumference.
If two chords in a circle are equal in length, then they will cut off equal arcs on the circumference. This is because the arcs that the chords cut off are subtended by the same central angle.
Learn more on circle theorem at:
https://brainly.com/question/6240879
#SPJ1
1/2 x^4=8
Solve the equation
Answers
Answer:
x=2
Step-by-step explanation:
x^4=16
x=[tex]\sqrt[4]{16}[/tex]
x=[tex]2[/tex]
3 out of 7 questions. PLEASE help me.
Answers
Translate the solid circle 2 units to the left and 2 units down and dilate the solid circle by a scale factor of 2. and the circles are similar
Transforming the circles(a) To move the solid circle exactly onto the dashed circle, we need to perform the following transformations:
Translate the solid circle 2 units to the left and 2 units down.Dilate the solid circle by a scale factor of 2.Therefore, the blank spaces should be filled as follows:
Translate the solid circle 2 units to the left and 2 units down.
Dilate the solid circle by a scale factor of 2.
(b) Yes, the original solid circle and the dashed circle are not similar, because they have different radii.
This is because all circles are similar
Read more about transformation at
https://brainly.com/question/27224272
#SPJ1
c. what is the probability that the duration of a rainfall event at this location is between 2 and 3 hours? d. what is the probability that a rainfall duration exceeds the mean value by more than 2 standard deviations?
Answers
The probability that a rainfall event exceeds the mean by more than 2 standard deviations is approximately 0.0498.
a. The exponential distribution with a mean of 2.725 hours can be expressed as λ = 1/2.725. Using this parameter, we can calculate the probabilities as follows:
P(X ≥ 2) = [tex]e^{(-λ2) }= e^{(-1/2.7252)[/tex] ≈ 0.4800
P(X ≤ 3) = 1 - [tex]e^{(-λ3)} = 1 - e^{(-1/2.7253)[/tex] ≈ 0.6674
P(2 ≤ X ≤ 3) = [tex]e^{(-λ2)} - e^{(-λ3)} = e^{(-1/2.7252)} - e^{(-1/2.7253)}[/tex] ≈ 0.1474
b. The standard deviation of an exponential distribution is equal to the mean, so 2 standard deviations above the mean would be 2*2.725 = 5.45 hours. The probability that a rainfall event exceeds this duration can be calculated as follows:
P(X > 5.45) =[tex]e^{(-λ5.45)} = e^{(-1/2.7255.45)}[/tex] ≈ 0.0498
Therefore, the probability that a rainfall event exceeds the mean by more than 2 standard deviations is approximately 0.0498.
Learn more about probability
https://brainly.com/question/24756209
#SPJ4
Complete Question:
Suppose that rainfall duration follows an exponential distribution with mean value 2.725 hours.
a. What is the probability that the duration of a particular rainfall event is at least 2 hours? At most 3 hours? Between 2 and 3 hours? (.4800, .6674, .1474)
b. What is the probability that rainfall duration exceeds the mean value by more than 2 standard deviations? (.0498)
9. Patricia has 5 cups of rice cereal. She
uses 3 cups of rice cereal to make
granola bars, then borrows 0.5 cup of
rice cereal from her friend. Her recipe
for cereal clusters calls for 3 cups of
rice cereal. Does Patricia have enough?
How much will she have left over, or
how much more will she need?
A Yes, she has 1/2cup left.
B No, she needs 1/2cup more.
C Yes, she 1/4 has cup left.
D No, she needs 1/4cup more.
Answers
Therefore, the correct answer is (B) No, she needs 1/2 cup more.
To determine if Patricia has enough rice cereal for her recipe, we need to calculate the total amount of rice cereal she has after all her actions and compare it to the 3 cups required for the cereal clusters.
Initially, Patricia had 5 cups of rice cereal. She used 3 cups to make granola bars, leaving her with 2 cups. She then borrowed 0.5 cup from her friend, which brings her total to 2.5 cups.
Finally, she needs 3 cups of rice cereal for the cereal clusters recipe. Since she only has 2.5 cups, she does not have enough rice cereal and needs to get more. Therefore, the correct answer is B) No, she needs 1/2 cup more.
She then borrows 0.5 cup, so she now has 2 + 0.5 = 2.5 cups.
needs 3 - 2.5 = 0.5 cups more.
To know more about amount visit:
https://brainly.com/question/22661325
#SPJ1
Maxine graphs the function m(x) which has a vertex of (-3,4) and passes through the point (-1,-8). Ricardo graphs p(x) = (x+3)² +4
Maxine thinks that both functions have the same axis of symmetry equation. Do you agree or disagree?
Answers
Both functions have the same axis of symmetry equation, which is x = -3.
Given that, Maxine graphs a function m(x) which has a vertex of (-3,4) and passes through the point (-1,-8).
Ricardo graphs p(x) = (x+3)² + 4
We need to check if both the function axis of symmetry equation.
So,
Both functions have a vertex of (-3,4), which means that the axis of symmetry must be a vertical line passing through x = -3.
Axis of symmetry = The axis of symmetry is an imaginary straight line that divides the shape into two identical parts or that makes the shape symmetrical.
For the function p(x) = (x+3)² +4, the axis of symmetry is indeed x = -3.
For the function m(x), since it has a vertex of (-3,4), the equation of the axis of symmetry is x = -3.
To know more about function,
brainly.com/question/28193995
#SPJ1
Fifteen children split $9 among themselves so that each child receives the same amount. How much did each child receive?
Answers
The total amount of money received by each child after splitting $9 among 15 children is equal to $0.60.
Total number of children is equal to 15
Total amount of money distributed among 15 children = $9
To find out how much each child receives,
We can divide the total amount of money by the number of children.
In this case, there are 15 children and $9 to split.
So, the amount of money each child receives is equal to,
(Total amount of money )/ ( total number of children )
= $9 ÷ 15
= $0.60
Therefore, amount of money received by each child in the group of 15 children is equal to $0.60.
Learn more about children here
brainly.com/question/159555
#SPJ4
what is the expected ratio of two heads : heads/tails : tails/heads : two tails when two coins are repeatedly flipped? (this question is asking about probability, which is a prediction, rather than your actual observed results.)
Answers
When two coins are repeatedly flipped, the probability of getting two heads is 1/4, the probability of getting a head and a tail is 1/2, and the probability of getting two tails is also 1/4.
Therefore, the expected ratio of two heads : heads/tails : tails/heads : two tails is 1:2:2:1, respectively. This means that out of every six flips, we would expect to see one outcome of two heads, two outcomes of heads/tails and tails/heads each, and one outcome of two tails.
However, it is important to note that this is only a prediction and the actual results may differ due to chance.
Learn more about probability:
https://brainly.com/question/24756209
#SPJ11
Which comparison is not correct?
A. 1 > -9
B. 3 < 6
C. -8 > -6
D. -3 < 4
Answers
Answer:
The comparison that is not correct is:
C. -8 > -6
This is not correct because -8 is actually less than -6. Therefore, the correct comparison would be -8 < -6.
The other comparisons are correct:
A. 1 > -9 (true, because 1 is greater than -9)
B. 3 < 6 (true, because 3 is less than 6)
D. -3 < 4 (true, because -3 is less than 4)
A rectangular garden has a walkway around it. The area of the garden is 4(4.5x+3.5). The combined area of the garden and the walkway is 5.5(6x+5). Find the area of the walkway around the garden as the sum of two terms.
Answers
The product of two terms gives the walkway's area around the garden: 15x+13.5.
Define rectangleA rectangle is a four-sided polygon with two pairs of parallel and congruent sides, and four right angles. The opposite sides of a rectangle are equal in length and parallel to each other, while the adjacent sides are perpendicular to each other.
Area of garden = 4(4.5x + 3.5) = 18x+14
The combined area of the garden and the walkway = 5.5(6x+5) =33x+27.5
The area of the walkway (Aw) around the garden is the result of subtracting the total area minus the inner area:
Aw=combined area -Area of garden
=33x+27.5-18x-14
=15x+13.5
Thus, we can say that the area of the walkway around the garden is the sum of two terms: 15x+13.5.
To know more about perpendicular, visit:
https://brainly.com/question/29268451
#SPJ1
Question:
The current (in amps) in a simple
electrical circuit varies inversely to
the resistance measured in ohms.
The current is 24 amps when the
resistance is 20 ohms. Find the
current (in amps) when the
resistance is 12 ohms.
Answers
The current in the circuit when the resistance is 12 ohms is 40 amps.
What is fraction?
A fraction is a mathematical term that represents a part of a whole or a ratio between two quantities.
We can use the inverse proportionality formula to solve this problem, which states that:
current (in amps) x resistance (in ohms) = constant
Let's call this constant "k". We can use the information given in the problem to find k:
24 amps x 20 ohms = k
k = 480
Now we can use this constant to find the current when the resistance is 12 ohms:
current x 12 ohms = 480
current = 480 / 12
current = 40 amps
Therefore, the current in the circuit when the resistance is 12 ohms is 40 amps.
To learn more about fraction from the given link:
https://brainly.com/question/10354322
#SPJ1