Charlie made the following table to record the height of each person in his family.

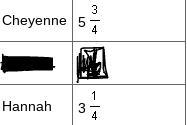
If Cheyenne and Hannah lay end to end, how far will they reach?

A. 9

B. 9, 1/2

C. 10

D. 8

Answer:

The formula for the area of a trapezoid is:

Area = (b1 + b2) / 2 x h

where b1 and b2 are the lengths of the two parallel bases, and h is the height.

We are given that the area of the trapezoid is 96 ft, the height is 8 ft, and one of the bases (b1) is 11 ft. We can use this information to find the length of the other base (b2).

Substituting the given values into the formula for the area of a trapezoid, we get:

96 = (11 + b2) / 2 x 8

Multiplying both sides by 2 and dividing by 8, we get:

24 = 11 + b2

Subtracting 11 from both sides, we get:

b2 = 13

Therefore, the length of the other base is 13 ft.

Therefore , the solution of the given problem of unitary method comes out to be during the 4-second period, the tram's elevation changed by 3 metres every second.

To complete the assignment, use the iii . -and-true basic technique, the real variables, and any pertinent details gathered from basic and specialised questions. In response, customers might be given another opportunity to sample expression the products. If these changes don't take place, we will miss out on important gains in our knowledge of programmes.

Here,

By dividing the overall elevation change (12 metres) by the total time required (4 seconds),

it is possible to determine the change in the tram's elevation every second. We would then have the average rate of elevation change per second.

=> Elevation change equals 12 metres

=> Total duration: 4 seconds

=>  12 meters / 4 seconds

=> 3 meters/second

As a result, during the 4-second period, the tram's elevation changed by 3 metres every second.

To know more about unitary method  visit:

https://brainly.com/question/28276953

#SPJ1  

When two coins are repeatedly flipped, the probability of getting two heads is 1/4, the probability of getting a head and a tail is 1/2, and the probability of getting two tails is also 1/4.

Therefore, the expected ratio of two heads : heads/tails : tails/heads : two tails is 1:2:2:1, respectively. This means that out of every six flips, we would expect to see one outcome of two heads, two outcomes of heads/tails and tails/heads each, and one outcome of two tails.

However, it is important to note that this is only a prediction and the actual results may differ due to chance.

Learn more about probability:

https://brainly.com/question/24756209

#SPJ11

To determine if each ordered pair is a point of intersection between the line x - y = 6 and the circle y² - 26 = -x², we need to substitute the values of x and y in both equations and see if they are true for both.

For the ordered pair (1, -5):

x - y = 6 becomes 1 - (-5) = 6, which is true.

y² - 26 = -x² becomes (-5)² - 26 = -(1)², which is false.

Therefore, (1, -5) is not a point of intersection.

For the ordered pair (1, 5):

x - y = 6 becomes 1 - 5 = -4, which is false.

y² - 26 = -x² becomes (5)² - 26 = -(1)², which is true.

Therefore, (1, 5) is a point of intersection.

For the ordered pair (5, -1):

x - y = 6 becomes 5 - (-1) = 6, which is true.

y² - 26 = -x² becomes (-1)² - 26 = -(5)², which is false.

Therefore, (5, -1) is not a point of intersection.

So the answer is:

(1,-5) - No

(1,5) - Yes

(5,-1) - No

to know more about equations

brainly.com/question/29657983

#SPJ1

Answer:

x=2

Step-by-step explanation:

x^4=16

x=[tex]\sqrt[4]{16}[/tex]

x=[tex]2[/tex]

The probability that a rainfall event exceeds the mean by more than 2 standard deviations is approximately 0.0498.

a. The exponential distribution with a mean of 2.725 hours can be expressed as λ = 1/2.725. Using this parameter, we can calculate the probabilities as follows:

P(X ≥ 2) = [tex]e^{(-λ2) }= e^{(-1/2.7252)[/tex] ≈ 0.4800

P(X ≤ 3) = 1 - [tex]e^{(-λ3)} = 1 - e^{(-1/2.7253)[/tex] ≈ 0.6674

P(2 ≤ X ≤ 3) = [tex]e^{(-λ2)} - e^{(-λ3)} = e^{(-1/2.7252)} - e^{(-1/2.7253)}[/tex] ≈ 0.1474

b. The standard deviation of an exponential distribution is equal to the mean, so 2 standard deviations above the mean would be 2*2.725 = 5.45 hours. The probability that a rainfall event exceeds this duration can be calculated as follows:

P(X > 5.45) =[tex]e^{(-λ5.45)} = e^{(-1/2.7255.45)}[/tex] ≈ 0.0498

Therefore, the probability that a rainfall event exceeds the mean by more than 2 standard deviations is approximately 0.0498.

Learn more about probability

https://brainly.com/question/24756209

#SPJ4

Complete Question:

Suppose that rainfall duration follows an exponential distribution with mean value 2.725 hours.

a. What is the probability that the duration of a particular rainfall event is at least 2 hours? At most 3 hours? Between 2 and 3 hours? (.4800, .6674, .1474)

b. What is the probability that rainfall duration exceeds the mean value by more than 2 standard deviations? (.0498)

The statement that is true about Evan's expression is that it represents a linear function of the amount of medicine in his bloodstream, where the initial amount is 100 milligrams and the rate of change is -0.4 milligrams per minute.

What is the equivalent expression?

Equivalent expressions are expressions that perform the same function despite their appearance. If two algebraic expressions are equivalent, they have the same value when we use the same variable value.

The expression 100 - 0.4m represents the amount of medicine in Evan's bloodstream after m minutes, where the amount of medicine decreases by 0.4 milligrams each minute.

The coefficient of the variable m (-0.4) represents the rate of change of the amount of medicine in Evan's bloodstream per minute. It tells us that for every one minute that passes, the amount of medicine in his bloodstream decreases by 0.4 milligrams.

The constant term (100) represents the initial amount of medicine in Evan's bloodstream before the medicine starts to decrease.

Therefore, the statement that is true about Evan's expression is that it represents a linear function of the amount of medicine in his bloodstream, where the initial amount is 100 milligrams and the rate of change is -0.4 milligrams per minute.

To learn more about the equivalent expression visit:

https://brainly.com/question/2972832

#SPJ1

The answer to the trigonometry question in the picture attached is:

   = cos θ / [sin θ * (1 - sin θ)] * (1 + sin θ)

Simplify 1-csc θ as follows:

1 - csc θ = (1 - csc θ)(1 + csc θ) / (1 + csc θ)

= 1 - csc^2 θ / (1 + csc θ)

= 1 - 1/sin^2 θ / (1 + 1/sin θ)

= 1 - sin^2 θ / (sin θ + 1)

= (sin θ - sin^2 θ) / (sin θ + 1)

Simplify 1+csc θ as follows:

1 + csc θ = (1 + csc θ)(1 - csc θ) / (1 - csc θ)

= 1 - csc^2 θ / (1 - csc θ)

= 1 - 1/sin^2 θ / (1 - 1/sin θ)

= 1 - sin^2 θ / (sin θ - 1)

= (sin θ + sin^2 θ) / (sin θ - 1)

Substitute the above simplifications in the expression cos θ/(1-csc θ) * 1+csc θ/(1+ csc θ) to get:

cos θ / (sin θ - sin^2 θ) * (sin θ + sin^2 θ) / (sin θ + 1)

Simplify the expression by canceling out the sin^2 θ terms:

cos θ / (sin θ - sin^2 θ) * (sin θ + sin^2 θ) / (sin θ + 1)

= cos θ / (sin θ - sin^2 θ) * (1 + sin θ) / (sin θ + 1)

Simplify further by factoring out common terms in the numerator and denominator:

cos θ / (sin θ - sin^2 θ) * (1 + sin θ) / (sin θ + 1)

= cos θ * (1 + sin θ) / [(sin θ - sin^2 θ) * (sin θ + 1)]

Finally, simplify the expression by factoring out a sin θ term from the denominator:

cos θ * (1 + sin θ) / [(sin θ - sin^2 θ) * (sin θ + 1)]

= cos θ * (1 + sin θ) / [sin θ * (1 - sin θ) * (sin θ + 1)]

= cos θ / [sin θ * (1 - sin θ)] * (1 + sin θ)

Learn more about Trigonometry here:

https://brainly.com/question/25618616

#SPJ1

(1) m∠1=45°(sum of 3 angles of a triangle is always 180°)

(2) m∠1=180°-129°=51°(sum of two interior angles on the same side is equal to the exterior angle)

(3) m∠1= 152°-115°=37°

(4) m∠1=88°m∠2=42° m∠3=113°

An angle is a geometric figure formed by two rays that share a common endpoint, called the vertex. The measure of an angle is typically expressed in degrees or radians, and it describes the amount of rotation needed to bring one of the rays into coincidence with the other.

A triangle is a closed two-dimensional shape with three straight sides and three angles.

(1) m∠1=45°(sum of 3 angles of a triangle is always 180°)

(2) m∠1=180°-129°=51°(sum of two interior angles on the same side is equal to the exterior angle)

(3) m∠1= 152°-115°=37°(sum of two interior angles on the same side is equal to the exterior angle)

(4) m∠1=88°(sum of 3 angles of a triangle is always 180°),m∠2=42°(vertically opposite angle theorem), m∠3=113°(sum of 3 angles of a triangle is always 180°)

Learn more about angles here:

https://brainly.com/question/28451077

#SPJ1

The correct statement about scale factor is the radius of the larger can will be 8 inches. (option c).

Let's first consider the dimensions of the small can of tomato paste. We are given that it has a radius of 2 inches and a height of 4 inches. Therefore, its volume can be calculated using the formula for the volume of a cylinder, which is V = πr²h, where V is the volume, r is the radius, and h is the height. Substituting the given values, we get:

V_small = π(2²)(4) = 16π cubic inches

Using these dimensions, we can calculate the volume of the larger can using the same formula:

V_large = π(6²)(12) = 432π cubic inches

Now, let's compare the volumes of the small and large cans. We have:

V_large = 432π cubic inches > 16π cubic inches = V_small

Therefore, we can conclude that the volume of the larger can is greater than the volume of the smaller can. But is it three times greater? Let's compare:

V_large = 432π cubic inches 3

V_small = 3(16π) cubic inches = 48π cubic inches

We see that 432π cubic inches is not equal to 48π cubic inches, so option b) is not correct.

Finally, let's consider the radius of the larger can. We found earlier that it is 6 inches, which is greater than the radius of the smaller can, but it is not 8 inches. Therefore, option c) is correct.

To know more about scale factor here

https://brainly.com/question/30215119

#SPJ4

Complete Question:

A small can of tomato paste has a radius of 2 inches and a height of 4 inches. Suppose the larger, commercial-size can has dimensions that are related by a scale factor of 3. Which of these true?

a) The radius of the larger can will be 5 inches.

b) The volume of the larger can will be 3 times the volume of the smaller can

c) The radius of the larger can will be 8 inches.

d) The volume of the larger can is 3 times the volume of smaller can

Using the fact that the triangles are similar we can see that the value of x is  36

We can see that the triangles are similar due to the same interior angles, then ther is a scale factor k between them.

So we can write:

20*k = 48

k = 48/20 = 2.4

Then:

x = 15*2.4

x = 36

That is the value of x.

Learn more about similar triangles at:

https://brainly.com/question/14285697

#SPJ1

The company should use the adjusted R² approach to select variables for their recommendation system, as it will better account for the influence of multiple variables and help create a more accurate model for predicting subscriber's movie ratings.

To build a successful movie recommendation system for the online media streaming company, it's important to consider the appropriate statistical approach for selecting variables.

In this case, the company should use the adjusted R² approach instead of the p-value approach.

The adjusted R² approach is more suitable for this scenario because it measures the proportion of variance in the dependent variable (subscriber's ratings) that is predictable from the independent variables (movie and subscriber data).

Adjusted R² takes into account the number of variables and adjusts for overfitting, which is important when dealing with a large dataset, like the one the streaming company has.

It helps in identifying the most influential factors and creating a model that better predicts movie ratings.
On the other hand, the p-value approach focuses on the statistical significance of individual variables, which might lead to including variables that are significant but not necessarily the best predictors for movie ratings.

This could result in a less accurate recommendation system.

For similar question on proportion.

https://brainly.com/question/11941144

#SPJ11

The action that would reduce the amount the person paid in taxes to 1,000 is option (D) Receiving a $49,000 tax credit

In this scenario, the person has $50,000 in taxable income and pays a 10% income tax rate, which amounts to $5,000 in taxes. To reduce the tax liability to $1,000, the person needs to receive a tax credit of $49,000. Tax credits directly reduce the amount of tax owed, whereas tax deductions reduce taxable income.

A tax deduction of $4,000 would lower the taxable income to $46,000, resulting in a lower tax liability of $4,600, which is not low enough to reach $1,000. Therefore, a tax credit of $49,000 is needed to reduce the tax liability to $1,000.

Therefore, the correct option is (D) Receiving a $49,000 tax credit

Learn more about tax credit here

brainly.com/question/30565676

#SPJ4

The given question is incomplete, the complete question is:

A person has $50,000 in taxable income for a year and pays a 10 percent income tax rate, equal to $5,000. Which action would reduce the amount the person paid in taxes to $1,000?

A.Receiving a $4,000 tax deduction

B.Receiving a $4,000 tax credit

C. Receiving a $49,000 tax deduction

D. Receiving a $49,000 tax credit

The inequality represented by the given number line is: -60 ≥ m.

We can see the values that an inequality represents by placing it on a number line.

On a number line, inequalities are represented by drawing a straight line and designating the end points as an open or closed circle.

On a number line, inequality is represented as follows:

For the given number line,

-6 is shown with the closed circle, with lines extending towards +∞

Thus, the inequality represented by the given number line is: -60 ≥ m.

Know more about the inequality

https://brainly.com/question/30853768

#SPJ1

Answer:

Step-by-step explanation:

5989.87

Answer:

The Correct answer is sinA/3.2=sin110°/4.6

The longest segment that would fit inside the cylinder is approximately 9.06 centimeters.

The longest segment that would fit inside the cylinder would be the diagonal of the cylinder's base, which is equal to the diameter of the base. The diameter of the base is equal to twice the radius, so it is 6 cm. Using the Pythagorean theorem, we can find the length of the diagonal:

[tex]diagonal^2 = radius^2 + height^2 \\diagonal^2 = 3^2 + 8^2 \\diagonal^2 = 9 + 64 \\diagonal^2 = 73 \\diagonal = sqrt(73)[/tex]

Therefore, the longest segment that would fit inside the cylinder is approximately 8.54 cm (rounded to the nearest hundredth).
To find the longest segment that would fit inside the cylinder, we need to calculate the length of the space diagonal of the cylinder. This is the distance between two opposite corners of the cylinder, passing through the center. We can use the Pythagorean theorem in 3D for this calculation.

The terms we'll use are:
- Radius (r): 3 cm
- Height (h): 8 cm

To find the space diagonal (d), we can use the following formula:

[tex]d = \sqrt{r^2 + r^2 + h^2}[/tex]
Plug in the values:

[tex]d = \sqrt{((3 cm)^2 + (3 cm)^2 + (8 cm)^2)} d = \sqrt{(9 cm^2 + 9 cm^2 + 64 cm^2)} d = \sqrt{(82 cm^2)}[/tex]
d ≈ 9.06 cm

Learn more about cylinder here:

https://brainly.com/question/23991640

#SPJ11

The longest segment that can fit inside the cylinder is. [tex]$\sqrt{73}$ cm[/tex].

The longest segment that can fit inside a cylinder is a diagonal that connects two opposite vertices of the cylinder.

The length of this diagonal by using the Pythagorean theorem.

Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle.

It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.

This theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, often called the Pythagorean equation:[1]

[tex]{\displaystyle a^{2}+b^{2}=c^{2}.}[/tex]

The theorem is named for the Greek philosopher Pythagoras, born around 570 BC.

The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem.

The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.

Consider a right triangle with legs equal to the radius.

[tex]$r$[/tex] and the height [tex]$h$[/tex] of the cylinder, and with the diagonal as the hypotenuse.

Then, by the Pythagorean theorem, the length of the diagonal is:

[tex]$\sqrt{r^2 + h^2} = \sqrt{3^2 + 8^2} = \sqrt{73}$[/tex]

For similar questions on cylinder

https://brainly.com/question/23935577

#SPJ11

The number of tiles that will be required to cover a floor with dimensions 2 meters by 3 meters is given as follows:

D. 120 tiles.

To obtain the area of a rectangle, you need to multiply its length by its width. The formula for the area of a rectangle is:

Area = Length x Width

The area of the floor is given as follows:

2 x 3 = 6 m².

The area in m² of each tile is given as follows:

0.25 x 0.2 = 0.05.

Hence the number of tiles that will be required to cover the floor is given as follows:

6/0.05 = 120 tiles.

More can be learned about the area of a rectangle at https://brainly.com/question/25292087

#SPJ1

[tex]7^{(1/3)}[/tex] is the equivalent expression to ∛7 with rational exponents.

What are rational exponents?

Rational exponents are exponents that are expressed as fractions. Specifically, a rational exponent of the form m/n is equivalent to taking the nth root of a number and then raising it to the power of m.

When we talk about rational exponents, we are referring to exponents that are written as fractions. Specifically, a rational exponent of the form m/n is equivalent to taking the nth root of a number and then raising it to the power of m.

So, in the case of ∛7, we can rewrite the cube root symbol (∛) as a rational exponent with a denominator of 3. That is, ∛7 can be expressed as [tex]7^{(1/3)}[/tex] , where the 1/3 exponent means "take the cube root of 7".

Therefore, [tex]7^{(1/3)}[/tex] is the equivalent expression to ∛7 with rational exponents.

To learn more about rationlal exponents from the given link:

https://brainly.com/question/3009444

#SPJ1

The point of intersection in the first quadrant is (3, 4) from the equation of circle.

We can start by substituting the equation of the line into the equation of the circle and solving for z and y.

The equation for the circle is:

(x - h)^2 + (y - k)^2 = r^2

Substituting h = 0, k = 3, and r = 3, we get:

x^2 + (y - 3)^2 = 9

Now, we substitute y = 2z + 3 into the equation:

x^2 + (2z + 3 - 3)^2 = 9

Simplifying, we get:

x^2 + 4z^2 = 9

Since we are looking for a point in the first quadrant, both x and z must be positive. We can solve for z in terms of x:

4z^2 = 9 - x^2

z^2 = (9 - x^2)/4

z = sqrt[(9 - x^2)/4]

Substituting this into the equation y = 2z + 3, we get:

y = 2sqrt[(9 - x^2)/4] + 3

To find the point of intersection in the first quadrant, we need to find a value of x that satisfies both this equation and the equation of the circle. We can substitute the equation for y into the equation for the circle:

x^2 + [2sqrt((9 - x^2)/4)]^2 = 9

Simplifying, we get:

x^2 + (9 - x^2)/2 = 9

Multiplying both sides by 2:

2x^2 + 9 - x^2 = 18

Solving for x:

x^2 = 9

x = 3

Substituting x = 3 into the equation for y, we get:

y = 2sqrt[(9 - 3^2)/4] + 3 = 4

Therefore, the point of intersection in the first quadrant is (3, 4).

Learn more about equation of circle below.

https://brainly.com/question/1506955

#SPJ1

The expression in terms of the first power of sine is 1 + 3[tex]sin^{4}[/tex]x - 3[tex]sin^{2}[/tex]x - [tex]sin^{6}[/tex]x. The solution has been obtained by using the trigonometric identities.

What are trigonometric identities?

All possible values of the variables in the equation must satisfy the equality condition known as a trigonometric identity. A triangle's side length and angle can be used to express a variety of unusual trigonometric identities.

We are given expression as [tex]cos^{6}[/tex] (x).

This can be written as a cosine function as  [tex](cos^{2} x)^{3}[/tex].

We know that [tex]sin^{2}[/tex]x + [tex]cos^{2}[/tex]x = 1.

So, we get

⇒ (1 - [tex]sin^{2}[/tex]x[tex])^{3}[/tex]

⇒ 1 + 3[tex]sin^{4}[/tex]x - 3[tex]sin^{2}[/tex]x - [tex]sin^{6}[/tex]x

Hence, the required expression has been obtained.

Learn more about trigonometric identities from the given link

https://brainly.com/question/3785172

#SPJ1

Answer:see below

Step-by-step explanation:

10.600

11.80000

12.17

13.48

14.4000

21. 1km=100m;0.5km=500m;0.1km=100m

22.50m=5000cm; 5m=500cm; 0.5m=50cm

Answer:

2.07 cm

Step-by-step explanation:

Hypotenuse = 2 cm

Adjacent side = a

Formula

cos θ = Hypotenuse/Adjacent side

cos 15 = 2/a

Note

The value of cos 15 is approximately 0.965.

0.965 = 2/a

a = 2/0.965

a = 2.07 cm ( approximately )

Both functions have the same axis of symmetry equation, which is x = -3.

Given that, Maxine graphs a function m(x) which has a vertex of (-3,4) and passes through the point (-1,-8).

Ricardo graphs p(x) = (x+3)² + 4

We need to check if both the function axis of symmetry equation.

So,

Both functions have a vertex of (-3,4), which means that the axis of symmetry must be a vertical line passing through x = -3.

Axis of symmetry = The axis of symmetry is an imaginary straight line that divides the shape into two identical parts or that makes the shape symmetrical.

For the function p(x) = (x+3)² +4, the axis of symmetry is indeed x = -3.

For the function m(x), since it has a vertex of (-3,4), the equation of the axis of symmetry is x = -3.

To know more about function,

brainly.com/question/28193995

#SPJ1

The psychologist finds that the estimated Cohen's d is  0.32, the t statistic is 2. 83, and r² is 0.073.  Using r² and the extension of Cohen's guidelines for interpreting the effect size using r², there is a small treatment effect.   job seeker finds that the estimated Cohen's d is 0.88, the t statistic is 7. 78, and r² is 0.479.Using r² and the extension of Cohen's guidelines for interpreting the effect size with r², there is a large treatment effect

To calculate the estimated Cohen's d, we use the formula

d = (M - M0) / SD

where M is the mean of the treatment group (job seekers who received training on using the Internet to find job listings), M0 is the mean of the control group (typical job seeker), and SD is the pooled standard deviation of the two groups. Using the given values, we have

M = 8.7 months

M0 = 7.4 months

SD = 4.1 months

So, d = (8.7 - 7.4) / 4.1 = 0.32

Using Cohen's guidelines for interpreting effect size with Cohen's d, a value of 0.2 is considered a small effect, 0.5 a medium effect, and 0.8 a large effect. Therefore, with an estimated Cohen's d of 0.32, there is a small treatment effect.

To calculate r², we use the formula

r² = t² / (t² + df)

where t is the t statistic, df is the degrees of freedom (n-2 for a two-group design), and n is the sample size. Using the given values for the Internet training group, we have

t = 2.83

n = 81

df = 79

So, r² = 2.83² / (2.83² + 79) = 0.073

Using the extension of Cohen's guidelines for interpreting effect size with r², a value of 0.01 is considered a small effect, 0.09 a medium effect, and 0.25 a large effect. Therefore, with an r² of 0.073, there is a small treatment effect.

For the job seekers who received training on interview skills, we can calculate Cohen's d and r² in a similar way

d = (M - M0) / SD = (8.1 - 7.4) / 0.8 = 0.88

t = 7.78

n = 81

df = 79

r² = 7.78² / (7.78² + 79) = 0.479

Using Cohen's guidelines for interpreting effect size with Cohen's d, a value of 0.2 is considered a small effect, 0.5 a medium effect, and 0.8 a large effect. Therefore, with an estimated Cohen's d of 0.88, there is a large treatment effect.

Using the extension of Cohen's guidelines for interpreting effect size with r², a value of 0.01 is considered a small effect, 0.09 a medium effect, and 0.25 a large effect. Therefore, with an  r² of 0.479, there is a medium to large treatment effect.

To know more about estimated Cohen's d:

https://brainly.com/question/31427772

#SPJ4

Answer:.317

.091

Small to med

Med

.875

.431

Large

Large

Step-by-step explanation:

Therefore, the correct answer is (B) No, she needs 1/2 cup more.

To determine if Patricia has enough rice cereal for her recipe, we need to calculate the total amount of rice cereal she has after all her actions and compare it to the 3 cups required for the cereal clusters.

Initially, Patricia had 5 cups of rice cereal. She used 3 cups to make granola bars, leaving her with 2 cups. She then borrowed 0.5 cup from her friend, which brings her total to 2.5 cups.

Finally, she needs 3 cups of rice cereal for the cereal clusters recipe. Since she only has 2.5 cups, she does not have enough rice cereal and needs to get more. Therefore, the correct answer is B) No, she needs 1/2 cup more.

She then borrows 0.5 cup, so she now has 2 + 0.5 = 2.5 cups.

needs 3 - 2.5 = 0.5 cups more.

To know more about amount visit:

https://brainly.com/question/22661325

#SPJ1

Answer:

C and D

Step-by-step explanation:

cosA = [tex]\frac{adjacent}{hypotenuse}[/tex] = [tex]\frac{AB}{AC}[/tex] = [tex]\frac{4}{5}[/tex] ⇒ C

sinA = [tex]\frac{opposite}{hypotenuse}[/tex] = [tex]\frac{BC}{AC}[/tex] = [tex]\frac{3}{5}[/tex] ⇒ D

The perimeter and the area of the regular polygon are 20 inches and 27.53 square inches.

The figure representing a regular polygon with five sides of same length, whose perimeter and area is well described by following formulas:

Perimeter

p = n · l

Area

A = (n · l · a) / 2

Where:

Where the apothema is:

a = 0.5 · l / tan (180° / n)

If we know that l = 4 in and n = 5, then the perimeter and the area of the polygon are:

Perimeter

p = 5 · (4 in)

p = 20 in

Area

a = 0.5 · (4 in) / tan (180° / 5)

a = 0.5 · (4 in) / tan 36°

a = 2.753 in

A = [5 · (4 in) · (2.753 in)] / 2

A = 27.53 in²

To learn more on area of regular polygons: https://brainly.com/question/12291395

#SPJ1

The total amount of money received by each child after splitting $9 among 15 children is equal to $0.60.

Total number of children is equal to 15

Total amount of money distributed among 15 children = $9

To find out how much each child receives,

We can divide the total amount of money by the number of children.

In this case, there are 15 children and $9 to split.

So, the amount of money each child receives is equal to,

(Total amount of money )/ ( total number of children )

= $9 ÷ 15

= $0.60

Therefore, amount of money received by each child in the group of 15 children is equal to $0.60.

Learn more about children here

brainly.com/question/159555

#SPJ4