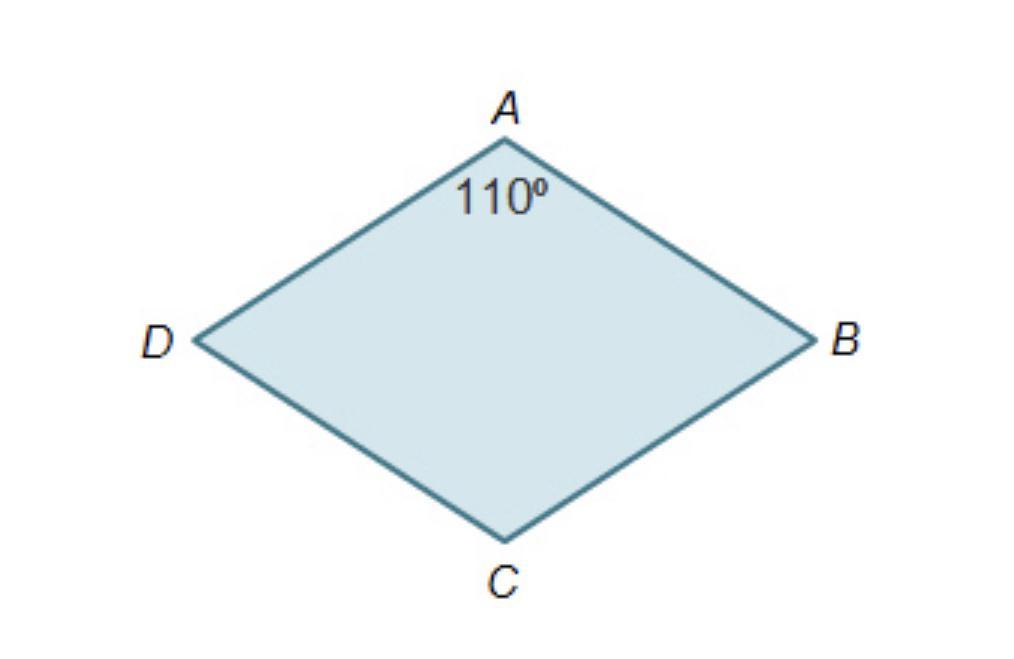
All sides are congruent in quadrilateral ABCD below.

Quadrilateral A B C D. Angle A is 110 degrees. Angle A is opposite to angle C.

How would this quadrilateral be best classified, and what is the measure of Angle B?
kite; Measure of angle B = 70 degrees
kite; Measure of angle B = 110 degrees
rhombus; Measure of angle B = 70 degrees
rhombus; Measure of angle B = 110 degrees

Answer:

28 feet

Step-by-step explanation:

area of a square = side times side; the sides are equal

50 = side times side or 50 = side^2

sqroot of 50 = sqroot of side^2

7 feet is about the size of the side of the square so using that information..

2 length + 2 width or 4 side

4 times 7 = 28

the perimeter is 28 feet

Hey Mate !

Here is your expert answer. If you do like this accurate answer. Please Mark as Brainliest !

Answer:

A 95% confidence interval estimate of the mean number of hours a legal professional works on a typical workday is [7.44 hours, 10.56 hours].

Step-by-step explanation:

We are given that x is normally distributed with a known standard deviation of 12.6.

A sample of 250 legal professionals was surveyed, and the sample's mean response was 9 hours.

Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;

                               P.Q.  =  [tex]\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }[/tex]  ~ N(0,1)

where, [tex]\bar X[/tex] = sample average mean response = 9 hours

            [tex]\sigma[/tex]  = population standard deviation = 12.6

            n = sample of legal professionals = 250

            [tex]\mu[/tex] = mean number of hours a legal professional works

Here for constructing a 95% confidence interval we have used One-sample z-test statistics as we know about population standard deviation.

So, 95% confidence interval for the population mean, [tex]\mu[/tex] is ;

P(-1.96 < N(0,1) < 1.96) = 0.95  {As the critical value of z at 2.5% level

                                                   of significance are -1.96 & 1.96}  

P(-1.96 < [tex]\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }[/tex] < 1.96) = 0.95

P( [tex]-1.96 \times {\frac{\sigma}{\sqrt{n} } }[/tex] < [tex]{\bar X-\mu}[/tex] < [tex]-1.96 \times {\frac{\sigma}{\sqrt{n} } }[/tex] ) = 0.95

P( [tex]\bar X-1.96 \times {\frac{\sigma}{\sqrt{n} } }[/tex] < [tex]\mu[/tex] < [tex]\bar X+1.96 \times {\frac{\sigma}{\sqrt{n} } }[/tex] ) = 0.95

95% confidence interval for [tex]\mu[/tex] = [ [tex]\bar X-1.96 \times {\frac{\sigma}{\sqrt{n} } }[/tex] , [tex]\bar X+1.96 \times {\frac{\sigma}{\sqrt{n} } }[/tex] ]

                                       = [ [tex]9-1.96 \times {\frac{12.6}{\sqrt{250} } }[/tex] , [tex]9+1.96 \times {\frac{12.6}{\sqrt{250} } }[/tex] ]

                                       = [7.44 hours, 10.56 hours]

Therefore, a 95% confidence interval estimate of the mean number of hours a legal professional works on a typical workday is [7.44 hours, 10.56 hours].

Answer:

A. $699.01

Step-by-step explanation:

130 = x − (0.042) (13547.92)

x = 699.01

Answer:

the absolute-value parent function has a slope of 1 on the right half.

I hope this will work fine for you.

Comment if you need more explanation

ThX

Step-by-step explanation:

Answer:

The ladder will reach 4.6 ft up the tree.

Step-by-step explanation:

When we draw out our triangle, we should see that we are given the horizontal leg and are trying to find the vertical leg. We use tan∅ to help solve:

tan53° = x/3.5

3.5tan53° = x

x = 4.64466

Answer:

-6p -10

Step-by-step explanation:

-12 - 6p - (-2)

Subtracting a negative is like adding

-12 - 6p + (2)

Combine like terms

-6p -12+2

-6p -10

Answer:

-6p=10

Step-by-step explanation:

-12 - 6p - (-2)  to combine like expression

-12-6p+2

-6p-10 to create equivalent expression an equal sign is used

-6p=10

Answer:

9p

Step-by-step explanation:

(x + p)(x + 9) =

= x^2 + 9x + px + 9p

= x^2 + (9 + p)x + 9p

The constant term is 9p.

Answer:

domain: (-4,4)

Step-by-step explanation:

i'm not sure if it has brackets because it doesn't have point that are on x-intervals -4 and 4

Answer:

D) -8

Step-by-step explanation:

If you add a positive and a negative, you end up subtracting. If your sum is lower than any of the numbers you are adding together, then there is a negative. In this case, your only negative number is -8, but if there were others, you could find this equation by doing negative six minus two (because the equation was originally addition, it would still be subtraction to check your work or find the answer in this case.)

Hopefully you find this useful :)

Answer:   -8

Step-by-step explanation:    lets take the unknown number as x,

so we have, 2 + x= -6

                 by using transposition method, x= -6-2( positive becomes  

                                                                       negative when transpositioning)

      so, x= -8                      

Answer:

The solution is x = 32.

Step-by-step explanation:

To solve the logarithmic equation [tex]\log _4\left(\frac{x}{2}\right)=2[/tex] you must:

Use the logarithmic definition [tex]\mathrm{If}\:\log _a\left(b\right)=c\:\mathrm{then}\:b=a^c[/tex].

[tex]\log _4\left(\frac{x}{2}\right)=2\quad \Rightarrow \quad \frac{x}{2}=4^2[/tex]

Multiply both sides by 2

[tex]\frac{x}{2}\cdot \:2=4^2\cdot \:2[/tex]

Simplify

[tex]x=32[/tex]

Hey there! :)

Answer:

The bag is cheaper because one litre is roughly $1.00, compared to the carton which is $1.99 for one litre.

Step-by-step explanation:

Given:

Bag of 4 litre milk = $3.99

Carton of 1 litre milk = $1.99

Find the price per litre for a bag of milk:

[tex]\frac{3.99}{4} = \frac{x}{1}[/tex]

Cross multiply:

3.99 = 4x

Divide both sides by 4:

3.99/4 = x.

x = 0.9975 ≈ $1.00

Bag of 1 litre milk ≈ $1.00

Carton of 1 litre milk = $1.99

$1.00 < $1.99

Therefore, the bag is cheaper.

Answer:

  1/275,625 ≈ 3.641×10^-6

Step-by-step explanation:

There are 65×65×65 = 274,625 possible combinations. The probability of guessing the correct one is 1/275,625 ≈ 3.641×10^-6.

Answer: A) Justification 1

Step-by-step explanation:

The student did not match the angles correctly.

∠ABC = 90° and ∠BCD = 60° so they cannot state that the angles are congruent. The other statement on that line is wrong also, but is irrelevant since there is already an error in that line.

Answer: 10 squares.

Step-by-step explanation:

We can do it with integrals.

If we take the bottom vertex as the point (0,0), the top right vertex as the point (0,4) and the left vertex as the point (5, 6)

then the area of the triangle is the area enclosed by two lines between the values x = 0 and x = 5.

the two lines are:

the bottom is the one that passes through (0,0) and (5,6)

f(x) = y = s*x (because it passes through the point (0,0))

and the slope is s = 6/5.

so f(x) =  y = (6/5)*x.

The top line is the one that passes through (0,4) and (5,6)

the y-intercept is b = 4, and the slope is:

s = (6 - 4)/(5 - 0) = 2/5.

g(x) = y = (2/5)*x + 4.

Now, the area enclosed for the triangle is equal to:

[tex]\int\limits^5_0 {g(x) - f(x)} \, dx[/tex]

this is equal to:

[tex]\int\limits^5_0 {(2/5)x + 4 - (6/5)x} \, dx = \int\limits^5_0 {-(4/5)*x + 4} \, dx[/tex]

= (1/2)(-4/5)*(5)^2 + 4*5 - 0 = 10

The area is 10 squares

Answer:

[tex]\mathbf{y(t) = t + \dfrac{7}{2}t^2 - \dfrac{2}{3}t^3+ ...}[/tex]

Step-by-step explanation:

THe interpretation of the given question is as follows:

y'' + ky +  ry³ = A cos ωt

Let k = 4, r = 3, A = 7 and ω = 8

The objective is to find the first three non zero terms in the Taylor polynomial approximation to the solution with initial values y(0) = 0 ; y' (0) = 1

SO;

y'' + ky " ry³ = A cos ωt

where;

k = 4, r = 3, A = 7 and ω = 8

y(0) = 0 ; y' (0) = 1

y'' + 4y + 3y³ = 7 cos 8t

y'' = - 4y - 3y³ + 7 cos 8t     ---- (1)

∴

y'' (0) = -4y(0) - 3y³(0) + 7 cos (0)

y'' (0) = - 4 × 0 - 3 × 0 + 7

y'' (0) = 7

Differentiating equation (1) with respect to  t ; we have:

y''' = - 4y' - 9y² × y¹ - 56 sin 8t

y''' (0) = -4y'(0) - 9y²(0)× y¹ (0) - 56 sin (0)

y''' (0) = - 4 × 1  - 9 × 0 × 1 - 56 × 0

y''' (0) = - 4

Thus; we have :

y(0) = 0  ; y'(0) = 1  ; y'' (0) = 7 ; y'''(0) = -4

Therefore; the Taylor polynomial approximation to the first three nonzero terms is :

[tex]y(t) = y(0) + y'(0) t + y''(0) \dfrac{t^2}{2!} + y'''(0) \dfrac{t^3}{3!}+...[/tex]

[tex]y(t) = 0 + t + 7 \dfrac{t^2}{2!} + \dfrac{-4}{3!} {t^3}+ ...[/tex]

[tex]\mathbf{y(t) = t + \dfrac{7}{2}t^2 - \dfrac{2}{3}t^3+ ...}[/tex]

Answer:

isoceles triangle

Step-by-step explanation:

All of these attributes fit an isoceles acute triangle.    An isoceles triangle needs 2 equal sides (which this description names) and 2 equal angles 80, 50, and 50.

Answer:

The answer is acute isosceles triangle

Step-by-step explanation:

Answer:

AC is four times longer than DF

Answer:

last option

Step-by-step explanation:

Let's say DF = x. DE = 2x which means DB is 4x. Since AC = DB the answer is the last option.

Answer: B. 22%

Step-by-step explanation:

Answer:

Yeah its 22%

Step-by-step explanation:

The question is incomplete. Here is the complete question.

A 50 gram sample of a substance that's used to treat thyroid disorders has a k-value of 0.1137. Find the substance's half-life, in days. Round your answer to the nearest tenth.

Answer: [tex]t_{1/2}[/tex] = 6.1 days

Step-by-step explanation: Half-life is the amount of time necessary for a substance to reduce to half of its initial value.

To determine half-life through mass of a substance:

[tex]N = N_{0}.e^{-kt_{1/2}}[/tex]

Initially, there are 50 grams. After 1 half-life, there are 25 grams:

[tex]25 = 50.e^{-0.1137.t_{1/2}}[/tex]

[tex]\frac{25}{50} = e^{-0.1137.t_{1/2}}[/tex]

[tex]\frac{1}{2} = e^{-0.1137.t_{1/2}}[/tex]

[tex]ln (\frac{1}{2} ) = ln (e^{-0.1137.t_{1/2}})[/tex]

ln(1) - ln(2) = -0.1137.[tex]t_{1/2}[/tex]

[tex]t_{1/2} = \frac{- ln(2)}{- 0.1137}[/tex]

[tex]t_{1/2} =[/tex] 6.1

The half-life of the sample substance is 6.1 days.

Answer:

The requirements that are necessary for a normal probability distribution to be a standard normal probability distribution are µ = 0 and σ = 1.

Step-by-step explanation:

A normal-distribution is an accurate symmetric-distribution of experimental data-values.  

If we create a histogram on data-values that are normally distributed, the figure of columns form a symmetrical bell shape.  

If X [tex]\sim[/tex] N (µ, σ²), then [tex]Z=\frac{X-\mu}{\sigma}[/tex], is a standard normal variate with mean, E (Z) = 0 and Var (Z) = 1. That is, Z [tex]\sim[/tex] N (0, 1).

The distribution of these z-variates is known as the standard normal distribution.

Thus, the requirements that are necessary for a normal probability distribution to be a standard normal probability distribution are µ = 0 and σ = 1.

Answer:

[tex] n * \frac{1}{2} = 95 [/tex]

Step-by-step explanation:

Required:

Select the equation that most accurately depicts the word problem

One-half of a certain number is 95.

Take the certain number to be n.

This statement in equation form will be:[tex] n * \frac{1}{2} = 95 [/tex]

Therefore, the equation that most accurately depicts the word problem is [tex] n * \frac{1}{2} = 95 [/tex]

Although your options are incomplete, but this answer is correct.

The * symbol can be replaced with a dot sign

Answer:

up up up up

Step-by-step explanation:

Answer:

Step-by-step explanation:

1/2x - 2/3 × 15 = 30

1/2x - 10 = 30

1/2x = 30 + 10

1/2x = 40

x = 40 × 2

x = 80

hope this helps

plz mark it bas brainliest!!!!!!!!!

Answer:

34

Step-by-step explanation:

uts obtuse angle

Answer:

16°

Step-by-step explanation:

Let x° be the missing angle:

cos x° = 53/55

cos x° = 0.963

using a calculator:

cos^(-1) (0.963) = 15.63 ≈ 16

Answer:A

Step-by-step explanation:

a. 2(3y - 2x) = 6y - 4x or rewritten as -4x + 6y

4x + 6y - 8 x

= 4x - 8x + 6y

= -4x + 6y

Answer:

[tex]\displaystyle m=2[/tex]

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

Algebra I

Step-by-step explanation:

Step 1: Define

Point (2, 8)

Point (-6, -8)

Step 2: Find slope m

Simply plug in the 2 coordinates into the slope formula to find slope m

Answer:

$11.81 EVERY Hour

Step-by-step explanation:

5 1/4 times 3

63/4 = 15 3/4

15 3/4 = 15.75 pounds of blueberries

15.75 x $0.75

11.81

Answer:

Division property of equality

Step-by-step explanation:

They are dividing both sides.

Answer:

1/64

Step-by-step explanation:

The probability of landing on a 7 is 1/8.

The probability of landing on a 2 is 1/8.

[tex]1/8 \times 1/8[/tex]

[tex]= 1/64[/tex]

1/64

The probability of landing on a 7 is 1/8.

The probability of landing on a 2 is 1/8.

1/8 \times 1/81/8×1/8

= 1/64=1/64

Answer:

The other polynomial is 11x^2 -3x

Step-by-step explanation:

12x^2 -5x  - ( x^2 -2x) = other polynomial

Distribute the minus sign

12x^2 -5x  -  x^2 +2x

Combine terms

11x^2 -3x

The other polynomial is 11x^2 -3x