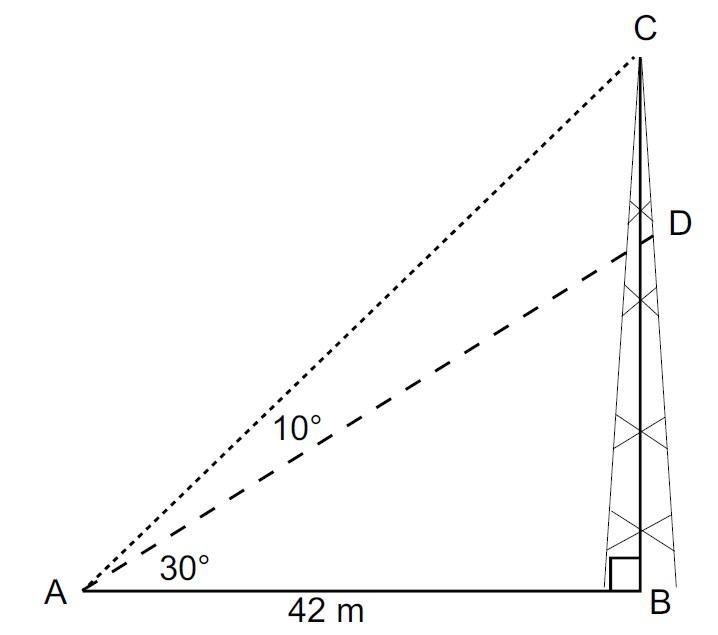
A communications tower is supported by two wires, connected at the same point on the ground. One is attached to the tower at D and the long-on at C. The angle AD makes with the ground is 30 ° and the angle between the two wires is 10 °. How much below the top of the tower is the shorter one attached?

Answer:

10.99 m

Step-by-step explanation:

✍️What we are basically asked to solve here is to find the distance between C and D.

To find CD, find the length of BC, and BD. Their difference will give us CD.

Thus, BC - BD = CD.

✍️Finding BC using trigonometric ratio formula:

[tex] \theta = 30 + 10 = 40 [/tex]

Opposite side = BC = ??

Adjacent side = 42 m

Thus:

[tex] tan(\theta) = \frac{opposite}{adjacent} [/tex]

Plug in the values

[tex] tan(40) = \frac{BC}{42} [/tex]

Multiply both sides by 42

[tex] tan(40) \times 42 = \frac{BC}{42} \times 42 [/tex]

[tex] 35.24 = BC [/tex]

BC = 35.24 m

✍️Finding BD using trigonometric ratio formula:

[tex] \theta = 30 [/tex]

Opposite side = BD = ??

Adjacent side = 42 m

Thus:

[tex] tan(\theta) = \frac{opposite}{adjacent} [/tex]

Plug in the values

[tex] tan(30) = \frac{BD}{42} [/tex]

Multiply both sides by 42

[tex] tan(30) \times 42 = \frac{BD}{42} \times 42 [/tex]

[tex] 24.25 = BD [/tex]

BD = 24.25 m

✍️How much below the top of the tower is the shorter one attached:

Thus,

BC - BD = CD

35.24 m - 24.25 m = 10.99 m

A wave is traveling with a speed of 500 m/sec and has a wavelength of 10 m. Determine its frequency.